This documentation page refers to a previous release of DIALS (2.2).
Click here to go to the corresponding page for the latest version of DIALS

DPF3 Part 2: A question of centring

Introduction

The second part of this tutorial continues from the results obtained in the DPF3 Part 1: Correcting poor initial geometry tutorial. You should work through that first to fix the incorrect beam centre recorded in the image headers and produce a correct indexing solution. Following those steps to the end will produce two files that we will take as the starting point here:

  • bravais_setting_5.expt - the experimental geometry including a crystal model with a primitive orthorhombic lattice
  • indexed.refl - the spot list from indexing

Viewing these files using the dials.image_viewer and the reciprocal lattice points in the dials.reciprocal_lattice_viewer reveals the presence of split spots and minor lattices. Nevertheless, these do not cause great difficulties in processing. More thought is required when considering the issue of possible pseudocentring. The structure can be solved in more than one space group. In cases such as this, the true symmetry may not be known until late stages of refinement. Even then, it might not be completely clear. Here we will investigate some features of the images that warn us of the challenges that lie ahead.

If we were to integrate this dataset using the oP solution from the first part and continue on to the CCP4 data reduction pipeline, we would see that Pointless chooses the space group \(P\,2_1\,2_1\,2_1\) but warns that the data were integrated on a primitive lattice, but may belong to a centered lattice. Accordingly, cTruncate finds strong evidence for translational NCS, for this basis along a vector of \((0.0, 0.5, 0.5)\). The fact that this vector corresponds to a half integral step along a face diagonal should lead us to question the space group assignment.

Questioning the lattice symmetry

It is always good advice to spend some time looking at the images and the reciprocal lattice before integrating a dataset. If we did so, we may notice the subtle features in the diffraction pattern that are the cause of the warnings from Pointless and cTruncate.

First the reciprocal lattice:

dials.reciprocal_lattice_viewer bravais_setting_5.expt indexed.refl
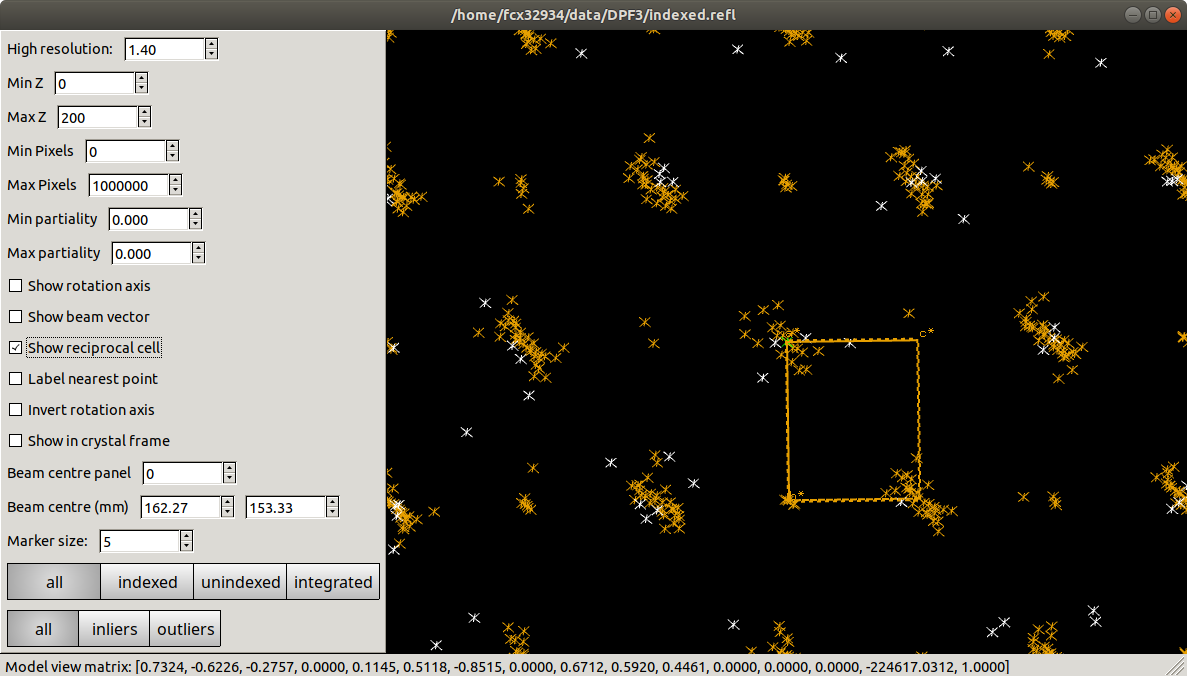
https://dials.github.io/images/centring_vs_pseudocentring/dpf3_oP_lo_res.png

Here the view has been aligned almost down the long axis of the reciprocal cell, which is \(a^\star\) for this choice of basis vectors. We see the columns of reciprocal lattice points with Miller indices differing by \(h\) as lines of closely-spaced points. However, we can also see that the lengths of the lines alternate between long and short as we move, for example, in the \(c^\star\) direction. At this point should suspect a pseudocentred lattice.

Now the image viewer:

dials.image_viewer bravais_setting_5.expt indexed.refl
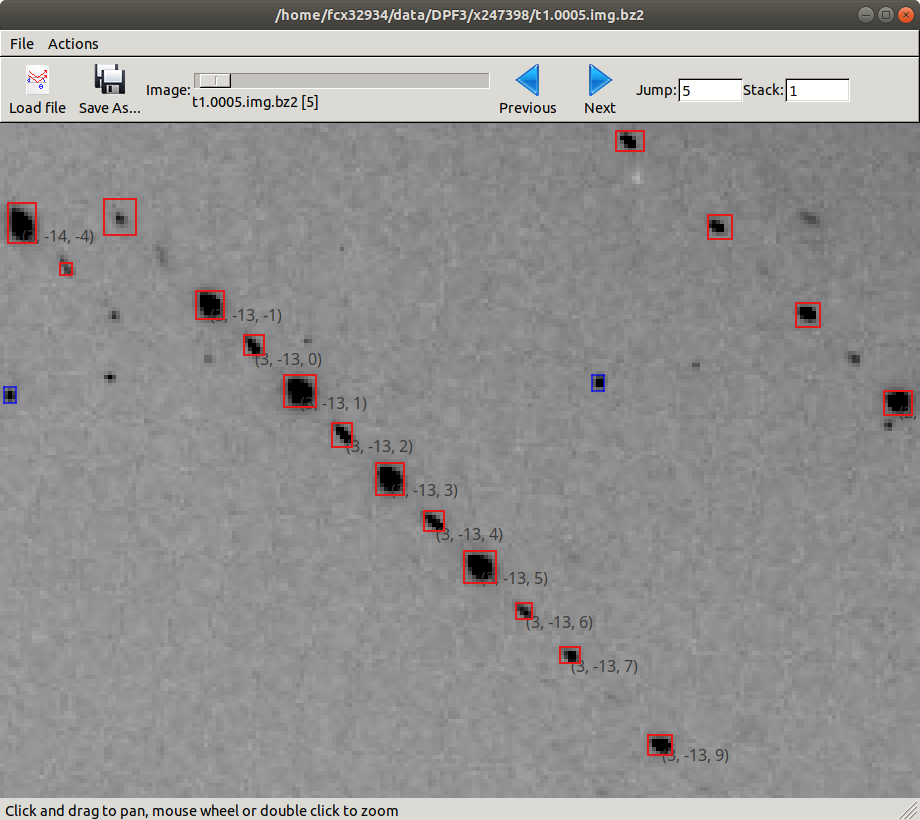
https://dials.github.io/images/centring_vs_pseudocentring/dpf3_oP_im5.png

Here we have zoomed in on a region of the central module on the 5th image. The line of indexed spots have Miller indices in \((3,-13,l)\). Looking closely we see that spots with even \(l\) are systematically weaker than spots with odd \(l\). This fits the theory of a pseudocentred lattice, however we also see that the spot profile differs between the two sets.

To investigate further we can enforce the centred lattice and see where that takes us…

Converting to a centred lattice

Although dials.refine_bravais_settings did not give us a centred lattice as an option, it is easy to convert the current primitive solution. First, note that for the currently chosen basis, the centring operation should be on the A face, not the conventional C face:

dials.reindex bravais_setting_5.expt space_group=A222

Here is part of the output:

New crystal:
Crystal:
    Unit cell: (56.277, 99.550, 121.252, 90.000, 90.000, 90.000)
    Space group: A 2 2 2

We now have a face centred space group, which we can use to index the strong reflections as follows:

dials.index reindexed.expt strong.refl

This produces a properly indexed spot list, but the space group is in an unconventional setting. We can fix this as follows:

dials.refine_bravais_settings indexed.expt indexed.refl

Solution 5 is what we want:

----------------------------------------------------------------------------------------------------------------
Solution Metric fit  rmsd  min/max cc #spots lattice                                 unit_cell volume      cb_op
----------------------------------------------------------------------------------------------------------------
*      5     0.0000 0.071 0.736/0.839  20000      oC  99.51 121.24  56.27  90.00  90.00  90.00 678839  b-c,b+c,a
*      4     0.0000 0.072 0.739/0.739  20000      mC  99.51 121.25  56.27  90.00  90.00  90.00 678994  b-c,b+c,a
*      3     0.0000 0.071 0.736/0.736  20000      mC 121.23  99.49  56.26  90.00  90.02  90.00 678556 b+c,-b+c,a
*      2     0.0000 0.069 0.839/0.839  20000      mP  78.35  56.24  78.39  90.00 101.24  90.00 338768    -c,-a,b
*      1     0.0000 0.070         -/-  20000      aP  56.22  78.38  78.34  78.75  90.00  90.01 338557      a,b,c
----------------------------------------------------------------------------------------------------------------

The table tells us that the indexed spots need a change of basis to be consistent with the conventional oC lattice:

dials.reindex indexed.refl change_of_basis_op=b-c,b+c,a

This gives us reindexed.refl. We can now pass this along with bravais_setting_5.expt to refinement and then to integration.

Centred or pseudocentred?

We have two ways we can model this crystal:

  • Primitive orthorhombic (\(P 2_1 2_1 2_1\)) with translational NCS mimicking centring on the C face
  • C-centred orthorhombic (\(C 2 2 2_1\)), ignoring the systematically weak intensities

The purpose of this exercise was mainly to demonstrate the use of DIALS viewers as diagnostic tools and some of the less commonly used options that allowed us to isolate the sub-lattice of strong reflections before integration.

If we continued with integration of the \(C 2 2 2_1\) data and proceeded onwards to structure solution, model rebuilding and refinement, then we would have reproduced the structure presented by PDB entry 5I3L. Refinement of this structure with isotropic B-factors against the \(C 2 2 2_1\) data integrated with DIALS results in an R-cryst of 0.18 and an R-free of 0.21.

On the contrary, if we had chosen the primitive lattice and included the systematically weak reflections in integration, the structure solution process would not have been straightforward and the results would be ambiguous, even if we would have used e.g. chain A of the PDB entry 5I3L as the search model for molecular replacement. Firstly, there would have been several different molecular replacement solutions with almost equal scores and subsequent refinement would favour \(P 2_1 2_1 2_1\) with a small margin of only a few percent in R factors compared to other solutions in space groups \(P 2 2 2_1\) and \(P 2_1 2_1 2\). In all these solutions the pseudo-translation vector relating two dimers would deviate by no more than 0.2 Angstroms from \((b+c)/2\) (this corresponds to the crystallographic translation \((a+b)/2\) in \(C 2 2 2_1\)). We did not try to rebuild the \(P 2_1 2_1 2_1\) solution but instead superposed two copies of the entire PDB entry 5I3L onto the two dimers forming its asymmetric unit. We ended up with R-cryst of 0.27 and R-free of 0.29, which are considerably worse than the values for the \(C 2 2 2_1\) structure.

There could be several reasons for poor refinement statistics in \(P 2_1 2_1 2_1\): the space group assignment was incorrect, the refinement program had problems with the weak structure amplitudes, or the crystal was partially disordered or has undergone a phase transition during data collection and it was not possible in the first place to describe the weak reflections with a single crystal structure. In any case, the ‘thorough’ \(P 2_1 2_1 2_1\) model gives no improvement in density or refinement statistics and provides no new structural information and we conclude that it should not be used for structural analysis. Ultimately it is true that for a real crystal any space group assignment is only an approximation.

Conclusions

  • Diffraction data may display a sub-lattice of weak spots (pseudocentring) indicating pseudo-translation in the crystal structure and, possibly, some degree of crystal disorder.
  • In many cases the weak reflections are not as weak as in this example and their intensities grow or oscillate with resolution. In those cases, good maps and refinement statistics can only be obtained by refinement against all the available data. It is important then to make sure that indexing picks up all the spots, strong and weak.
  • In many other cases, similar to the current example, the weak spots have no practical meaning and should be excluded. Ideally this should be done before the integration, which we did here in the section Converting to a centred lattice.
  • Use the DIALS viewers to make sure you know what to expect from your data!

Acknowledgements

Thanks to Wolfram Tempel for making this dataset available and inspiring the writing of this tutorial. Thanks also to Andrey Lebedev for detailed analysis of the primitive versus the centred lattice structures.