Please click here to go to the tutorial for DIALS 2.2.
Processing in Detail¶
Introduction¶
DIALS processing may be performed by either running the individual tools (spot
finding, indexing, refinement, integration, symmetry, scaling, exporting to MTZ)
or you can run xia2 pipeline=dials, which makes informed choices for you
at each stage. In this tutorial we will run through each of the steps in turn,
checking the output as we go. We will also enforce the correct lattice symmetry.
Tutorial data¶
The following example uses a Beta-Lactamase dataset collected using beamline I04 at Diamond Light Source, and reprocessed especially for these tutorials.
Hint
If you are physically at Diamond on the CCP4 Workshop, then
this data is already available in your training data area. After
typing module load ccp4-workshop you’ll be moved to a working
folder, with the data already located in the tutorial-data/summed
subdirectory.
The data is otherwise available for download from 
.
We’ll only be using the first run of data in this tutorial,
C2sum_1.tar, extracted to a tutorial-data/summed subdirectory.
Import¶
The first stage of step-by-step DIALS processing is to import the data - all that happens here is that metadata are read for all the images, and a file describing their contents (imported.expt) is written:
dials.import tutorial-data/summed/C2sum_1*.cbf.gz
The output just describes what the software understands of the images it was passed, in this case one sequence of data containing 720 images:
DIALS 3.dev.1293-g7efd2982c
The following parameters have been modified:
input {
experiments = <image files>
}
--------------------------------------------------------------------------------
format: <class 'dxtbx.format.FormatCBFMiniPilatusDLS6MSN100.FormatCBFMiniPilatusDLS6MSN100'>
template: /dls/mx-scratch/dials/tutorial_data/betalactamase_summed/C2sum_1_####.cbf.gz:1:720
num images: 720
sequences:
still: 0
sweep: 1
num stills: 0
--------------------------------------------------------------------------------
Writing experiments to imported.expt
Now is a good point to take a first look at the data using the dials.image_viewer, both to check that the data is sensible and to anticipate any problems in processing:
dials.image_viewer imported.expt
You will be presented with the main image viewer screen:
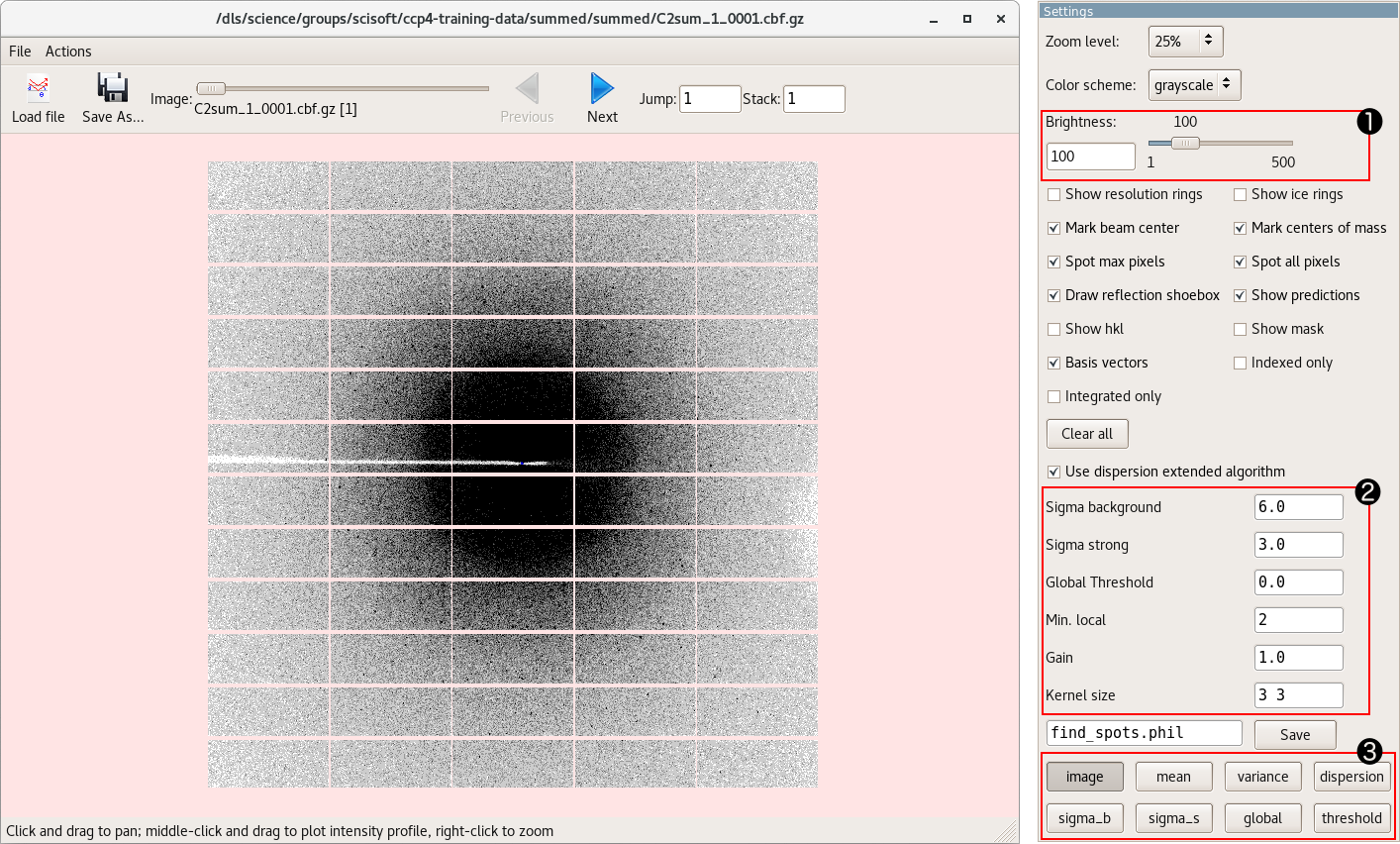
Play with the brightness slider (①) a little until you can clearly see the spots on the first image (something in the range 10-20 should make the spots obvious). You can also change the colour scheme (sometimes spots can be easier to identify in ‘inverted’ mode) , toggle various information markers like beam center, and try different configurations for the spot finding (②).
Find Spots¶
The first “real” task in any processing using DIALS is the spot finding. Since this is looking for spots on every image in the dataset, this process can take some time, so DIALS will use multiple processors by default to speed this up. Here we have limited it to 4, but feel free to omit this to let DIALS make the choice:
dials.find_spots imported.expt nproc=4
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3
4spotfinder {
5 mp {
6 nproc = 4
7 }
8}
9input {
10 experiments = imported.expt
11}
12
13Setting spotfinder.filter.min_spot_size=3
14Configuring spot finder from input parameters
15--------------------------------------------------------------------------------
16Finding strong spots in imageset 0
17--------------------------------------------------------------------------------
18
19Finding spots in image 1 to 720...
20Setting chunksize=20
21Extracting strong pixels from images
22 Using multiprocessing with 4 parallel job(s)
23
24Found 1818 strong pixels on image 1
25Found 1577 strong pixels on image 2
26Found 1461 strong pixels on image 3
27Found 1458 strong pixels on image 4
28Found 1738 strong pixels on image 5
29Found 1669 strong pixels on image 6
30Found 1671 strong pixels on image 7
31Found 1743 strong pixels on image 8
32Found 1664 strong pixels on image 9
33Found 1637 strong pixels on image 10
34Found 1475 strong pixels on image 11
35Found 1538 strong pixels on image 12
36Found 1521 strong pixels on image 13
37Found 1612 strong pixels on image 14
38Found 1565 strong pixels on image 15
39Found 1636 strong pixels on image 16
40Found 1474 strong pixels on image 17
41Found 1452 strong pixels on image 18
42Found 1489 strong pixels on image 19
43Found 1467 strong pixels on image 20
44Found 1599 strong pixels on image 21
45Found 1616 strong pixels on image 22
46Found 1430 strong pixels on image 23
47Found 1452 strong pixels on image 24
48Found 1549 strong pixels on image 25
49Found 1544 strong pixels on image 26
50Found 1538 strong pixels on image 27
51Found 1507 strong pixels on image 28
52Found 1488 strong pixels on image 29
53Found 1460 strong pixels on image 30
54Found 1571 strong pixels on image 31
55Found 1666 strong pixels on image 32
56Found 1463 strong pixels on image 33
57Found 1525 strong pixels on image 34
58Found 1499 strong pixels on image 35
59Found 1309 strong pixels on image 36
60Found 1276 strong pixels on image 37
61Found 1405 strong pixels on image 38
62Found 1432 strong pixels on image 39
63Found 1491 strong pixels on image 40
64Found 1443 strong pixels on image 41
65Found 1452 strong pixels on image 42
66Found 1459 strong pixels on image 43
67Found 1426 strong pixels on image 44
68Found 1445 strong pixels on image 45
69Found 1283 strong pixels on image 46
70Found 1350 strong pixels on image 47
71Found 1541 strong pixels on image 48
72Found 1496 strong pixels on image 49
73Found 1507 strong pixels on image 50
74Found 1324 strong pixels on image 51
75Found 1501 strong pixels on image 52
76Found 1470 strong pixels on image 53
77Found 1580 strong pixels on image 54
78Found 1457 strong pixels on image 55
79Found 1340 strong pixels on image 56
80Found 1217 strong pixels on image 57
81Found 1418 strong pixels on image 58
82Found 1356 strong pixels on image 59
83Found 1363 strong pixels on image 60
84Found 1312 strong pixels on image 61
85Found 1366 strong pixels on image 62
86Found 1373 strong pixels on image 63
87Found 1322 strong pixels on image 64
88Found 1407 strong pixels on image 65
89Found 1562 strong pixels on image 66
90Found 1362 strong pixels on image 67
91Found 1442 strong pixels on image 68
92Found 1362 strong pixels on image 69
93Found 1307 strong pixels on image 70
94Found 1535 strong pixels on image 71
95Found 1274 strong pixels on image 72
96Found 1355 strong pixels on image 73
97Found 1385 strong pixels on image 74
98Found 1303 strong pixels on image 75
99Found 1478 strong pixels on image 76
100Found 1470 strong pixels on image 77
101Found 1359 strong pixels on image 78
102Found 1364 strong pixels on image 79
103Found 1440 strong pixels on image 80
104Found 1397 strong pixels on image 81
105Found 1264 strong pixels on image 82
106Found 1424 strong pixels on image 83
107Found 1362 strong pixels on image 84
108Found 1412 strong pixels on image 85
109Found 1540 strong pixels on image 86
110Found 1276 strong pixels on image 87
111Found 1613 strong pixels on image 88
112Found 1433 strong pixels on image 89
113Found 1316 strong pixels on image 90
114Found 1407 strong pixels on image 91
115Found 1515 strong pixels on image 92
116Found 1444 strong pixels on image 93
117Found 1427 strong pixels on image 94
118Found 1346 strong pixels on image 95
119Found 1406 strong pixels on image 96
120Found 1455 strong pixels on image 97
121Found 1582 strong pixels on image 98
122Found 1307 strong pixels on image 99
123Found 1336 strong pixels on image 100
124Found 1394 strong pixels on image 101
125Found 1645 strong pixels on image 102
126Found 1587 strong pixels on image 103
127Found 1456 strong pixels on image 104
128Found 1512 strong pixels on image 105
129Found 1512 strong pixels on image 106
130Found 1450 strong pixels on image 107
131Found 1468 strong pixels on image 108
132Found 1643 strong pixels on image 109
133Found 1456 strong pixels on image 110
134Found 1347 strong pixels on image 111
135Found 1354 strong pixels on image 112
136Found 1770 strong pixels on image 113
137Found 1563 strong pixels on image 114
138Found 1467 strong pixels on image 115
139Found 1347 strong pixels on image 116
140Found 1488 strong pixels on image 117
141Found 1588 strong pixels on image 118
142Found 1476 strong pixels on image 119
143Found 1447 strong pixels on image 120
144Found 1508 strong pixels on image 121
145Found 1534 strong pixels on image 122
146Found 1434 strong pixels on image 123
147Found 1483 strong pixels on image 124
148Found 1475 strong pixels on image 125
149Found 1625 strong pixels on image 126
150Found 1524 strong pixels on image 127
151Found 1354 strong pixels on image 128
152Found 1387 strong pixels on image 129
153Found 1519 strong pixels on image 130
154Found 1535 strong pixels on image 131
155Found 1445 strong pixels on image 132
156Found 1560 strong pixels on image 133
157Found 1419 strong pixels on image 134
158Found 1567 strong pixels on image 135
159Found 1477 strong pixels on image 136
160Found 1638 strong pixels on image 137
161Found 1718 strong pixels on image 138
162Found 1430 strong pixels on image 139
163Found 1386 strong pixels on image 140
164Found 1523 strong pixels on image 141
165Found 1556 strong pixels on image 142
166Found 1526 strong pixels on image 143
167Found 1603 strong pixels on image 144
168Found 1710 strong pixels on image 145
169Found 1471 strong pixels on image 146
170Found 1682 strong pixels on image 147
171Found 1677 strong pixels on image 148
172Found 1692 strong pixels on image 149
173Found 1694 strong pixels on image 150
174Found 1580 strong pixels on image 151
175Found 1556 strong pixels on image 152
176Found 1630 strong pixels on image 153
177Found 1645 strong pixels on image 154
178Found 1716 strong pixels on image 155
179Found 1676 strong pixels on image 156
180Found 1720 strong pixels on image 157
181Found 1788 strong pixels on image 158
182Found 1530 strong pixels on image 159
183Found 1529 strong pixels on image 160
184Found 1474 strong pixels on image 161
185Found 1636 strong pixels on image 162
186Found 1650 strong pixels on image 163
187Found 1676 strong pixels on image 164
188Found 1624 strong pixels on image 165
189Found 1679 strong pixels on image 166
190Found 1534 strong pixels on image 167
191Found 1680 strong pixels on image 168
192Found 1689 strong pixels on image 169
193Found 1519 strong pixels on image 170
194Found 1789 strong pixels on image 171
195Found 1825 strong pixels on image 172
196Found 1591 strong pixels on image 173
197Found 1591 strong pixels on image 174
198Found 1671 strong pixels on image 175
199Found 1648 strong pixels on image 176
200Found 1578 strong pixels on image 177
201Found 1803 strong pixels on image 178
202Found 1596 strong pixels on image 179
203Found 1655 strong pixels on image 180
204Found 1634 strong pixels on image 181
205Found 1679 strong pixels on image 182
206Found 1577 strong pixels on image 183
207Found 1677 strong pixels on image 184
208Found 1692 strong pixels on image 185
209Found 1525 strong pixels on image 186
210Found 1654 strong pixels on image 187
211Found 1485 strong pixels on image 188
212Found 1833 strong pixels on image 189
213Found 1845 strong pixels on image 190
214Found 1774 strong pixels on image 191
215Found 1621 strong pixels on image 192
216Found 1574 strong pixels on image 193
217Found 1512 strong pixels on image 194
218Found 1944 strong pixels on image 195
219Found 1843 strong pixels on image 196
220Found 1760 strong pixels on image 197
221Found 1433 strong pixels on image 198
222Found 1618 strong pixels on image 199
223Found 1780 strong pixels on image 200
224Found 1714 strong pixels on image 201
225Found 1710 strong pixels on image 202
226Found 1705 strong pixels on image 203
227Found 1496 strong pixels on image 204
228Found 1458 strong pixels on image 205
229Found 1680 strong pixels on image 206
230Found 1559 strong pixels on image 207
231Found 1624 strong pixels on image 208
232Found 1859 strong pixels on image 209
233Found 1795 strong pixels on image 210
234Found 1543 strong pixels on image 211
235Found 1621 strong pixels on image 212
236Found 1639 strong pixels on image 213
237Found 1451 strong pixels on image 214
238Found 1737 strong pixels on image 215
239Found 1744 strong pixels on image 216
240Found 1720 strong pixels on image 217
241Found 1629 strong pixels on image 218
242Found 1793 strong pixels on image 219
243Found 1647 strong pixels on image 220
244Found 1873 strong pixels on image 221
245Found 1787 strong pixels on image 222
246Found 1835 strong pixels on image 223
247Found 1709 strong pixels on image 224
248Found 1719 strong pixels on image 225
249Found 1552 strong pixels on image 226
250Found 1721 strong pixels on image 227
251Found 1990 strong pixels on image 228
252Found 1742 strong pixels on image 229
253Found 1752 strong pixels on image 230
254Found 1573 strong pixels on image 231
255Found 1629 strong pixels on image 232
256Found 1774 strong pixels on image 233
257Found 1668 strong pixels on image 234
258Found 1652 strong pixels on image 235
259Found 1649 strong pixels on image 236
260Found 1840 strong pixels on image 237
261Found 1695 strong pixels on image 238
262Found 1712 strong pixels on image 239
263Found 1758 strong pixels on image 240
264Found 1815 strong pixels on image 241
265Found 1770 strong pixels on image 242
266Found 1841 strong pixels on image 243
267Found 1832 strong pixels on image 244
268Found 1606 strong pixels on image 245
269Found 1695 strong pixels on image 246
270Found 1684 strong pixels on image 247
271Found 1818 strong pixels on image 248
272Found 1893 strong pixels on image 249
273Found 1708 strong pixels on image 250
274Found 1634 strong pixels on image 251
275Found 1605 strong pixels on image 252
276Found 1618 strong pixels on image 253
277Found 1772 strong pixels on image 254
278Found 1523 strong pixels on image 255
279Found 1646 strong pixels on image 256
280Found 1846 strong pixels on image 257
281Found 1608 strong pixels on image 258
282Found 1838 strong pixels on image 259
283Found 1832 strong pixels on image 260
284Found 1758 strong pixels on image 261
285Found 1486 strong pixels on image 262
286Found 1590 strong pixels on image 263
287Found 1726 strong pixels on image 264
288Found 1523 strong pixels on image 265
289Found 1779 strong pixels on image 266
290Found 2014 strong pixels on image 267
291Found 2008 strong pixels on image 268
292Found 1720 strong pixels on image 269
293Found 1931 strong pixels on image 270
294Found 1680 strong pixels on image 271
295Found 1683 strong pixels on image 272
296Found 1802 strong pixels on image 273
297Found 2017 strong pixels on image 274
298Found 1963 strong pixels on image 275
299Found 1701 strong pixels on image 276
300Found 1706 strong pixels on image 277
301Found 1664 strong pixels on image 278
302Found 1863 strong pixels on image 279
303Found 1931 strong pixels on image 280
304Found 1765 strong pixels on image 281
305Found 1656 strong pixels on image 282
306Found 1593 strong pixels on image 283
307Found 1685 strong pixels on image 284
308Found 1791 strong pixels on image 285
309Found 1723 strong pixels on image 286
310Found 1726 strong pixels on image 287
311Found 1582 strong pixels on image 288
312Found 1813 strong pixels on image 289
313Found 1755 strong pixels on image 290
314Found 1842 strong pixels on image 291
315Found 1736 strong pixels on image 292
316Found 1779 strong pixels on image 293
317Found 1802 strong pixels on image 294
318Found 1536 strong pixels on image 295
319Found 1616 strong pixels on image 296
320Found 1619 strong pixels on image 297
321Found 1729 strong pixels on image 298
322Found 1867 strong pixels on image 299
323Found 1835 strong pixels on image 300
324Found 1917 strong pixels on image 301
325Found 1621 strong pixels on image 302
326Found 1722 strong pixels on image 303
327Found 1571 strong pixels on image 304
328Found 1566 strong pixels on image 305
329Found 1490 strong pixels on image 306
330Found 1633 strong pixels on image 307
331Found 1703 strong pixels on image 308
332Found 1623 strong pixels on image 309
333Found 1608 strong pixels on image 310
334Found 1631 strong pixels on image 311
335Found 1682 strong pixels on image 312
336Found 1742 strong pixels on image 313
337Found 1697 strong pixels on image 314
338Found 1599 strong pixels on image 315
339Found 1538 strong pixels on image 316
340Found 1620 strong pixels on image 317
341Found 1733 strong pixels on image 318
342Found 1817 strong pixels on image 319
343Found 1513 strong pixels on image 320
344Found 1489 strong pixels on image 321
345Found 1514 strong pixels on image 322
346Found 1551 strong pixels on image 323
347Found 1705 strong pixels on image 324
348Found 1868 strong pixels on image 325
349Found 1694 strong pixels on image 326
350Found 1586 strong pixels on image 327
351Found 1619 strong pixels on image 328
352Found 1527 strong pixels on image 329
353Found 1763 strong pixels on image 330
354Found 1555 strong pixels on image 331
355Found 1417 strong pixels on image 332
356Found 1491 strong pixels on image 333
357Found 1760 strong pixels on image 334
358Found 1284 strong pixels on image 335
359Found 1460 strong pixels on image 336
360Found 1571 strong pixels on image 337
361Found 1439 strong pixels on image 338
362Found 1530 strong pixels on image 339
363Found 1525 strong pixels on image 340
364Found 1577 strong pixels on image 341
365Found 1370 strong pixels on image 342
366Found 1572 strong pixels on image 343
367Found 1422 strong pixels on image 344
368Found 1483 strong pixels on image 345
369Found 1267 strong pixels on image 346
370Found 1454 strong pixels on image 347
371Found 1526 strong pixels on image 348
372Found 1537 strong pixels on image 349
373Found 1363 strong pixels on image 350
374Found 1562 strong pixels on image 351
375Found 1470 strong pixels on image 352
376Found 1413 strong pixels on image 353
377Found 1591 strong pixels on image 354
378Found 1473 strong pixels on image 355
379Found 1437 strong pixels on image 356
380Found 1572 strong pixels on image 357
381Found 1418 strong pixels on image 358
382Found 1245 strong pixels on image 359
383Found 1515 strong pixels on image 360
384Found 1575 strong pixels on image 361
385Found 1608 strong pixels on image 362
386Found 1358 strong pixels on image 363
387Found 1348 strong pixels on image 364
388Found 1570 strong pixels on image 365
389Found 1429 strong pixels on image 366
390Found 1497 strong pixels on image 367
391Found 1706 strong pixels on image 368
392Found 1496 strong pixels on image 369
393Found 1402 strong pixels on image 370
394Found 1264 strong pixels on image 371
395Found 1459 strong pixels on image 372
396Found 1492 strong pixels on image 373
397Found 1447 strong pixels on image 374
398Found 1498 strong pixels on image 375
399Found 1344 strong pixels on image 376
400Found 1387 strong pixels on image 377
401Found 1376 strong pixels on image 378
402Found 1299 strong pixels on image 379
403Found 1324 strong pixels on image 380
404Found 1405 strong pixels on image 381
405Found 1428 strong pixels on image 382
406Found 1276 strong pixels on image 383
407Found 1372 strong pixels on image 384
408Found 1283 strong pixels on image 385
409Found 1435 strong pixels on image 386
410Found 1487 strong pixels on image 387
411Found 1381 strong pixels on image 388
412Found 1472 strong pixels on image 389
413Found 1453 strong pixels on image 390
414Found 1484 strong pixels on image 391
415Found 1403 strong pixels on image 392
416Found 1355 strong pixels on image 393
417Found 1419 strong pixels on image 394
418Found 1320 strong pixels on image 395
419Found 1284 strong pixels on image 396
420Found 1334 strong pixels on image 397
421Found 1298 strong pixels on image 398
422Found 1392 strong pixels on image 399
423Found 1431 strong pixels on image 400
424Found 1284 strong pixels on image 401
425Found 1291 strong pixels on image 402
426Found 1342 strong pixels on image 403
427Found 1498 strong pixels on image 404
428Found 1395 strong pixels on image 405
429Found 1262 strong pixels on image 406
430Found 1333 strong pixels on image 407
431Found 1451 strong pixels on image 408
432Found 1353 strong pixels on image 409
433Found 1385 strong pixels on image 410
434Found 1232 strong pixels on image 411
435Found 1452 strong pixels on image 412
436Found 1431 strong pixels on image 413
437Found 1431 strong pixels on image 414
438Found 1392 strong pixels on image 415
439Found 1270 strong pixels on image 416
440Found 1220 strong pixels on image 417
441Found 1471 strong pixels on image 418
442Found 1270 strong pixels on image 419
443Found 1308 strong pixels on image 420
444Found 1166 strong pixels on image 421
445Found 1356 strong pixels on image 422
446Found 1219 strong pixels on image 423
447Found 1334 strong pixels on image 424
448Found 1287 strong pixels on image 425
449Found 1520 strong pixels on image 426
450Found 1234 strong pixels on image 427
451Found 1298 strong pixels on image 428
452Found 1250 strong pixels on image 429
453Found 1358 strong pixels on image 430
454Found 1481 strong pixels on image 431
455Found 1128 strong pixels on image 432
456Found 1287 strong pixels on image 433
457Found 1379 strong pixels on image 434
458Found 1222 strong pixels on image 435
459Found 1416 strong pixels on image 436
460Found 1343 strong pixels on image 437
461Found 1264 strong pixels on image 438
462Found 1358 strong pixels on image 439
463Found 1411 strong pixels on image 440
464Found 1339 strong pixels on image 441
465Found 1151 strong pixels on image 442
466Found 1376 strong pixels on image 443
467Found 1309 strong pixels on image 444
468Found 1348 strong pixels on image 445
469Found 1347 strong pixels on image 446
470Found 1264 strong pixels on image 447
471Found 1501 strong pixels on image 448
472Found 1356 strong pixels on image 449
473Found 1300 strong pixels on image 450
474Found 1378 strong pixels on image 451
475Found 1413 strong pixels on image 452
476Found 1240 strong pixels on image 453
477Found 1257 strong pixels on image 454
478Found 1369 strong pixels on image 455
479Found 1265 strong pixels on image 456
480Found 1307 strong pixels on image 457
481Found 1371 strong pixels on image 458
482Found 1276 strong pixels on image 459
483Found 1236 strong pixels on image 460
484Found 1334 strong pixels on image 461
485Found 1434 strong pixels on image 462
486Found 1546 strong pixels on image 463
487Found 1324 strong pixels on image 464
488Found 1456 strong pixels on image 465
489Found 1393 strong pixels on image 466
490Found 1294 strong pixels on image 467
491Found 1229 strong pixels on image 468
492Found 1551 strong pixels on image 469
493Found 1322 strong pixels on image 470
494Found 1252 strong pixels on image 471
495Found 1346 strong pixels on image 472
496Found 1563 strong pixels on image 473
497Found 1419 strong pixels on image 474
498Found 1288 strong pixels on image 475
499Found 1288 strong pixels on image 476
500Found 1365 strong pixels on image 477
501Found 1538 strong pixels on image 478
502Found 1369 strong pixels on image 479
503Found 1324 strong pixels on image 480
504Found 1336 strong pixels on image 481
505Found 1394 strong pixels on image 482
506Found 1235 strong pixels on image 483
507Found 1305 strong pixels on image 484
508Found 1308 strong pixels on image 485
509Found 1498 strong pixels on image 486
510Found 1364 strong pixels on image 487
511Found 1172 strong pixels on image 488
512Found 1217 strong pixels on image 489
513Found 1411 strong pixels on image 490
514Found 1389 strong pixels on image 491
515Found 1314 strong pixels on image 492
516Found 1407 strong pixels on image 493
517Found 1365 strong pixels on image 494
518Found 1517 strong pixels on image 495
519Found 1315 strong pixels on image 496
520Found 1399 strong pixels on image 497
521Found 1444 strong pixels on image 498
522Found 1220 strong pixels on image 499
523Found 1203 strong pixels on image 500
524Found 1367 strong pixels on image 501
525Found 1388 strong pixels on image 502
526Found 1421 strong pixels on image 503
527Found 1371 strong pixels on image 504
528Found 1612 strong pixels on image 505
529Found 1312 strong pixels on image 506
530Found 1487 strong pixels on image 507
531Found 1478 strong pixels on image 508
532Found 1399 strong pixels on image 509
533Found 1537 strong pixels on image 510
534Found 1444 strong pixels on image 511
535Found 1360 strong pixels on image 512
536Found 1441 strong pixels on image 513
537Found 1413 strong pixels on image 514
538Found 1526 strong pixels on image 515
539Found 1486 strong pixels on image 516
540Found 1516 strong pixels on image 517
541Found 1545 strong pixels on image 518
542Found 1368 strong pixels on image 519
543Found 1472 strong pixels on image 520
544Found 1358 strong pixels on image 521
545Found 1377 strong pixels on image 522
546Found 1497 strong pixels on image 523
547Found 1359 strong pixels on image 524
548Found 1409 strong pixels on image 525
549Found 1479 strong pixels on image 526
550Found 1335 strong pixels on image 527
551Found 1549 strong pixels on image 528
552Found 1500 strong pixels on image 529
553Found 1314 strong pixels on image 530
554Found 1568 strong pixels on image 531
555Found 1630 strong pixels on image 532
556Found 1352 strong pixels on image 533
557Found 1460 strong pixels on image 534
558Found 1504 strong pixels on image 535
559Found 1489 strong pixels on image 536
560Found 1391 strong pixels on image 537
561Found 1577 strong pixels on image 538
562Found 1526 strong pixels on image 539
563Found 1449 strong pixels on image 540
564Found 1541 strong pixels on image 541
565Found 1478 strong pixels on image 542
566Found 1392 strong pixels on image 543
567Found 1517 strong pixels on image 544
568Found 1455 strong pixels on image 545
569Found 1411 strong pixels on image 546
570Found 1448 strong pixels on image 547
571Found 1344 strong pixels on image 548
572Found 1659 strong pixels on image 549
573Found 1720 strong pixels on image 550
574Found 1648 strong pixels on image 551
575Found 1478 strong pixels on image 552
576Found 1458 strong pixels on image 553
577Found 1409 strong pixels on image 554
578Found 1815 strong pixels on image 555
579Found 1730 strong pixels on image 556
580Found 1682 strong pixels on image 557
581Found 1400 strong pixels on image 558
582Found 1449 strong pixels on image 559
583Found 1612 strong pixels on image 560
584Found 1581 strong pixels on image 561
585Found 1652 strong pixels on image 562
586Found 1530 strong pixels on image 563
587Found 1422 strong pixels on image 564
588Found 1444 strong pixels on image 565
589Found 1591 strong pixels on image 566
590Found 1406 strong pixels on image 567
591Found 1478 strong pixels on image 568
592Found 1765 strong pixels on image 569
593Found 1698 strong pixels on image 570
594Found 1535 strong pixels on image 571
595Found 1505 strong pixels on image 572
596Found 1597 strong pixels on image 573
597Found 1500 strong pixels on image 574
598Found 1772 strong pixels on image 575
599Found 1626 strong pixels on image 576
600Found 1642 strong pixels on image 577
601Found 1455 strong pixels on image 578
602Found 1650 strong pixels on image 579
603Found 1450 strong pixels on image 580
604Found 1894 strong pixels on image 581
605Found 1751 strong pixels on image 582
606Found 1755 strong pixels on image 583
607Found 1697 strong pixels on image 584
608Found 1667 strong pixels on image 585
609Found 1543 strong pixels on image 586
610Found 1709 strong pixels on image 587
611Found 1886 strong pixels on image 588
612Found 1691 strong pixels on image 589
613Found 1718 strong pixels on image 590
614Found 1653 strong pixels on image 591
615Found 1565 strong pixels on image 592
616Found 1807 strong pixels on image 593
617Found 1543 strong pixels on image 594
618Found 1652 strong pixels on image 595
619Found 1584 strong pixels on image 596
620Found 1884 strong pixels on image 597
621Found 1630 strong pixels on image 598
622Found 1678 strong pixels on image 599
623Found 1777 strong pixels on image 600
624Found 1994 strong pixels on image 601
625Found 1766 strong pixels on image 602
626Found 1954 strong pixels on image 603
627Found 1767 strong pixels on image 604
628Found 1591 strong pixels on image 605
629Found 1686 strong pixels on image 606
630Found 1774 strong pixels on image 607
631Found 1816 strong pixels on image 608
632Found 1779 strong pixels on image 609
633Found 1701 strong pixels on image 610
634Found 1643 strong pixels on image 611
635Found 1579 strong pixels on image 612
636Found 1676 strong pixels on image 613
637Found 1804 strong pixels on image 614
638Found 1716 strong pixels on image 615
639Found 1772 strong pixels on image 616
640Found 1898 strong pixels on image 617
641Found 1600 strong pixels on image 618
642Found 1851 strong pixels on image 619
643Found 1724 strong pixels on image 620
644Found 1772 strong pixels on image 621
645Found 1696 strong pixels on image 622
646Found 1686 strong pixels on image 623
647Found 1770 strong pixels on image 624
648Found 1530 strong pixels on image 625
649Found 1779 strong pixels on image 626
650Found 1977 strong pixels on image 627
651Found 2011 strong pixels on image 628
652Found 1824 strong pixels on image 629
653Found 1956 strong pixels on image 630
654Found 1741 strong pixels on image 631
655Found 1793 strong pixels on image 632
656Found 1793 strong pixels on image 633
657Found 2019 strong pixels on image 634
658Found 2019 strong pixels on image 635
659Found 1844 strong pixels on image 636
660Found 1767 strong pixels on image 637
661Found 1781 strong pixels on image 638
662Found 1965 strong pixels on image 639
663Found 2000 strong pixels on image 640
664Found 1977 strong pixels on image 641
665Found 1745 strong pixels on image 642
666Found 1686 strong pixels on image 643
667Found 1740 strong pixels on image 644
668Found 1832 strong pixels on image 645
669Found 1813 strong pixels on image 646
670Found 1782 strong pixels on image 647
671Found 1683 strong pixels on image 648
672Found 1828 strong pixels on image 649
673Found 1744 strong pixels on image 650
674Found 1931 strong pixels on image 651
675Found 1796 strong pixels on image 652
676Found 1813 strong pixels on image 653
677Found 1932 strong pixels on image 654
678Found 1573 strong pixels on image 655
679Found 1710 strong pixels on image 656
680Found 1751 strong pixels on image 657
681Found 1779 strong pixels on image 658
682Found 1814 strong pixels on image 659
683Found 1810 strong pixels on image 660
684Found 2067 strong pixels on image 661
685Found 1659 strong pixels on image 662
686Found 1711 strong pixels on image 663
687Found 1669 strong pixels on image 664
688Found 1660 strong pixels on image 665
689Found 1699 strong pixels on image 666
690Found 1774 strong pixels on image 667
691Found 1776 strong pixels on image 668
692Found 1646 strong pixels on image 669
693Found 1655 strong pixels on image 670
694Found 1665 strong pixels on image 671
695Found 1721 strong pixels on image 672
696Found 1802 strong pixels on image 673
697Found 1673 strong pixels on image 674
698Found 1697 strong pixels on image 675
699Found 1621 strong pixels on image 676
700Found 1686 strong pixels on image 677
701Found 1774 strong pixels on image 678
702Found 1865 strong pixels on image 679
703Found 1675 strong pixels on image 680
704Found 1654 strong pixels on image 681
705Found 1481 strong pixels on image 682
706Found 1635 strong pixels on image 683
707Found 1768 strong pixels on image 684
708Found 1800 strong pixels on image 685
709Found 1697 strong pixels on image 686
710Found 1581 strong pixels on image 687
711Found 1672 strong pixels on image 688
712Found 1601 strong pixels on image 689
713Found 1819 strong pixels on image 690
714Found 1611 strong pixels on image 691
715Found 1588 strong pixels on image 692
716Found 1615 strong pixels on image 693
717Found 1793 strong pixels on image 694
718Found 1476 strong pixels on image 695
719Found 1610 strong pixels on image 696
720Found 1576 strong pixels on image 697
721Found 1470 strong pixels on image 698
722Found 1659 strong pixels on image 699
723Found 1604 strong pixels on image 700
724Found 1730 strong pixels on image 701
725Found 1625 strong pixels on image 702
726Found 1596 strong pixels on image 703
727Found 1509 strong pixels on image 704
728Found 1528 strong pixels on image 705
729Found 1392 strong pixels on image 706
730Found 1560 strong pixels on image 707
731Found 1684 strong pixels on image 708
732Found 1600 strong pixels on image 709
733Found 1557 strong pixels on image 710
734Found 1659 strong pixels on image 711
735Found 1582 strong pixels on image 712
736Found 1625 strong pixels on image 713
737Found 1613 strong pixels on image 714
738Found 1637 strong pixels on image 715
739Found 1549 strong pixels on image 716
740Found 1734 strong pixels on image 717
741Found 1541 strong pixels on image 718
742Found 1271 strong pixels on image 719
743Found 1568 strong pixels on image 720
744
745Extracted 129281 spots
746Removed 17040 spots with size < 3 pixels
747Removed 1 spots with size > 1000 pixels
748Calculated 112240 spot centroids
749Calculated 112240 spot intensities
750Filtered 112023 of 112240 spots by peak-centroid distance
751
752Histogram of per-image spot count for imageset 0:
753112023 spots found on 720 images (max 2192 / bin)
754* * * *
755************* ************* ****
756************************************************************
757************************************************************
758************************************************************
759************************************************************
760************************************************************
761************************************************************
762************************************************************
763************************************************************
7641 image 720
765
766--------------------------------------------------------------------------------
767Saved 112023 reflections to strong.refl
Once this has completed, a new reflection file
‘strong.refl’ is written, containing a record of every spot found.
The dials.image_viewer tool is not as fast as viewers such as ADXV, however it does integrate well with DIALS data files. Having found strong spots open the image viewer again, but giving it the newly found reflection list:
dials.image_viewer imported.expt strong.refl
Adjust the brightness so that you can see the spots, then zoom in so that you can see the clustered individual pixels of a single spot. Pixels determined to be part of a spot’s peak are marked with green dots. The blue outline shows the three-dimensional shoebox - the extents over detector x, y and image number z of a all peak pixels in a single spot. The single highest value pixel for any spot is marked with a pink circle, and the centre of mass is marked with a red cross.
The spot centre-of-mass is usually close to the peak pixel, but slightly offset as the algorithm allows calculation of the spot centre at a better precision than the pixel size and image angular ‘width’.
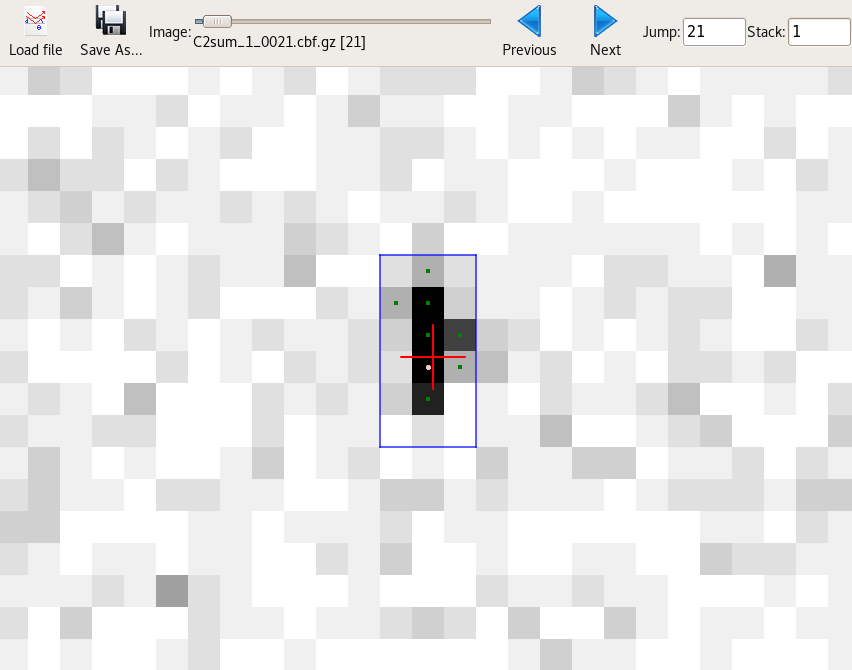
The default parameters for spot finding usually do a good job for Pilatus images, such as these. However they may not be optimal for data from other detector types, such as CCDs or image plates. Issues with incorrectly set gain might, for example, lead to background noise being extracted as spots. You can use the image mode buttons (③) to preview how the parameters affect the spot finding algorithm. The final image, ‘threshold’ is the one on which spots were found, so ensuring this produces peaks at real diffraction spot positions will give the best chance of success.
Another very powerful tool for investigating problems with strong spot positions is dials.reciprocal_lattice_viewer. This displays the strong spots in 3D, after mapping them from their detector positions to reciprocal space. In a favourable case you should be able to see the crystal’s reciprocal lattice by eye in the strong spot positions. Some practice may be needed in rotating the lattice to an orientation that shows off the periodicity in reciprocal lattice positions:
dials.reciprocal_lattice_viewer imported.expt strong.refl
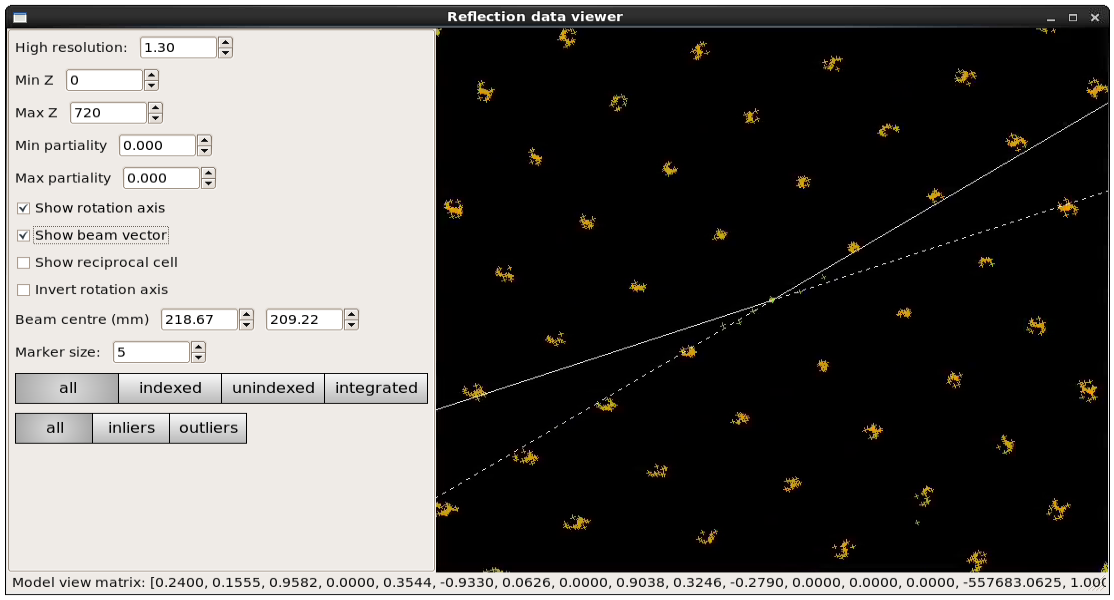
Although the reciprocal spacing is visible, in this data, there are clearly some systematic distortions. These will be solved in the indexing.
Indexing¶
The next step will be indexing of the strong spots by
dials.index, which by default uses a
3D FFT algorithm (although the 1D FFT algorithm can be selected, using the
parameter indexing.method=fft1d). We pass in all the strong
spots found in the dataset:
dials.index imported.expt strong.refl
If known, the space group and unit cell can be provided at this stage
using the space_group and unit_cell parameters, and will
be used to constrain the lattice during refinement, but otherwise
indexing and refinement will be carried out in the primitive lattice
using space group P1.
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3
4input {
5 experiments = imported.expt
6 reflections = strong.refl
7}
8
9Found max_cell: 94.4 Angstrom
10Setting d_min: 1.84
11FFT gridding: (256,256,256)
12Number of centroids used: 94547
13Candidate solutions:
14+----------------------------------+----------+----------------+------------+-------------+-------------------+-----------+-----------------+-----------------+
15| unit_cell | volume | volume score | #indexed | % indexed | % indexed score | rmsd_xy | rmsd_xy score | overall score |
16|----------------------------------+----------+----------------+------------+-------------+-------------------+-----------+-----------------+-----------------|
17| 40.57 40.76 69.67 91.8 91.9 98.5 | 113802 | 0.01 | 97056 | 98 | 0.01 | 0.07 | 0 | 0.02 |
18| 40.57 40.69 69.61 91.9 91.9 98.4 | 113520 | 0 | 96791 | 98 | 0.02 | 0.07 | 0 | 0.02 |
19| 40.69 40.81 69.67 92.1 91.9 98.2 | 114348 | 0.01 | 97693 | 99 | 0 | 0.07 | 0.02 | 0.04 |
20| 40.67 40.71 69.67 91.9 91.9 98.1 | 114067 | 0.01 | 97943 | 99 | 0 | 0.08 | 0.03 | 0.04 |
21| 40.71 40.94 69.67 91.8 91.9 98.3 | 114761 | 0.02 | 97041 | 98 | 0.01 | 0.07 | 0.01 | 0.04 |
22| 40.64 40.88 69.67 91.8 92.0 98.1 | 114433 | 0.01 | 97201 | 98 | 0.01 | 0.07 | 0.02 | 0.05 |
23| 40.71 40.75 69.59 91.9 91.8 98.2 | 114134 | 0.01 | 96927 | 98 | 0.02 | 0.08 | 0.02 | 0.05 |
24| 40.69 40.73 69.61 91.9 91.9 98.2 | 114048 | 0.01 | 97158 | 98 | 0.01 | 0.08 | 0.03 | 0.05 |
25| 40.69 40.77 69.67 92.0 91.9 98.2 | 114223 | 0.01 | 97782 | 99 | 0 | 0.08 | 0.04 | 0.05 |
26| 40.71 40.75 69.67 91.9 91.9 98.2 | 114263 | 0.01 | 97891 | 99 | 0 | 0.08 | 0.04 | 0.05 |
27| 40.69 40.71 69.61 91.9 92.0 98.1 | 113996 | 0.01 | 96838 | 98 | 0.02 | 0.08 | 0.03 | 0.05 |
28| 40.49 40.76 69.67 91.8 91.8 98.3 | 113654 | 0 | 95648 | 97 | 0.03 | 0.07 | 0.02 | 0.05 |
29| 40.69 40.78 69.61 91.6 91.9 98.2 | 114205 | 0.01 | 95594 | 96 | 0.04 | 0.07 | 0.01 | 0.06 |
30| 40.69 40.78 69.63 91.8 91.9 98.2 | 114232 | 0.01 | 97300 | 98 | 0.01 | 0.08 | 0.04 | 0.06 |
31| 40.69 40.71 69.67 91.9 91.9 98.1 | 114103 | 0.01 | 97769 | 99 | 0 | 0.08 | 0.05 | 0.06 |
32| 40.69 40.90 69.61 91.8 91.9 98.1 | 114530 | 0.02 | 96099 | 97 | 0.03 | 0.07 | 0.02 | 0.06 |
33| 40.64 40.69 69.63 92.0 91.9 98.0 | 113870 | 0.01 | 96429 | 97 | 0.02 | 0.08 | 0.03 | 0.06 |
34| 40.65 40.85 69.67 91.9 91.9 98.1 | 114381 | 0.01 | 97470 | 98 | 0.01 | 0.08 | 0.04 | 0.06 |
35| 40.69 40.71 69.65 91.8 92.1 98.1 | 114072 | 0.01 | 95912 | 97 | 0.03 | 0.08 | 0.02 | 0.06 |
36| 40.69 40.78 69.67 91.9 91.9 98.2 | 114289 | 0.01 | 97735 | 99 | 0 | 0.08 | 0.05 | 0.06 |
37| 40.71 40.76 69.67 91.8 91.9 98.4 | 114233 | 0.01 | 97389 | 98 | 0.01 | 0.08 | 0.05 | 0.06 |
38| 40.66 40.69 69.60 92.0 91.9 98.0 | 113880 | 0.01 | 96140 | 97 | 0.03 | 0.08 | 0.03 | 0.07 |
39| 40.70 40.79 69.57 92.0 91.9 98.1 | 114200 | 0.01 | 96531 | 97 | 0.02 | 0.08 | 0.03 | 0.07 |
40| 40.69 40.71 69.61 91.8 91.9 98.1 | 114011 | 0.01 | 96503 | 97 | 0.02 | 0.08 | 0.04 | 0.07 |
41| 40.69 40.70 69.67 91.9 91.9 98.1 | 114073 | 0.01 | 97591 | 98 | 0.01 | 0.08 | 0.05 | 0.07 |
42| 40.71 40.75 69.58 91.9 91.9 98.2 | 114120 | 0.01 | 96940 | 98 | 0.01 | 0.08 | 0.04 | 0.07 |
43| 40.69 40.78 69.67 91.7 91.9 98.2 | 114298 | 0.01 | 96985 | 98 | 0.01 | 0.08 | 0.04 | 0.07 |
44| 40.69 40.71 69.54 91.9 91.9 98.1 | 113891 | 0.01 | 95976 | 97 | 0.03 | 0.08 | 0.03 | 0.07 |
45| 40.71 40.81 69.67 91.8 91.9 98.2 | 114433 | 0.01 | 97252 | 98 | 0.01 | 0.08 | 0.04 | 0.07 |
46| 40.57 40.69 69.61 91.9 91.8 98.2 | 113581 | 0 | 96179 | 97 | 0.03 | 0.08 | 0.04 | 0.07 |
47| 40.71 40.75 69.63 92.1 91.8 98.2 | 114196 | 0.01 | 96793 | 98 | 0.02 | 0.08 | 0.04 | 0.07 |
48| 40.64 40.82 69.58 92.0 92.0 98.2 | 114119 | 0.01 | 96882 | 98 | 0.02 | 0.08 | 0.05 | 0.07 |
49| 40.71 40.74 69.54 92.0 91.9 98.0 | 114044 | 0.01 | 96096 | 97 | 0.03 | 0.08 | 0.04 | 0.07 |
50| 40.69 40.78 69.61 91.7 91.9 98.2 | 114197 | 0.01 | 96456 | 97 | 0.02 | 0.08 | 0.04 | 0.07 |
51| 40.69 40.71 69.54 91.9 92.0 98.2 | 113844 | 0.01 | 96187 | 97 | 0.03 | 0.08 | 0.04 | 0.08 |
52| 40.76 40.81 69.67 92.1 91.8 98.4 | 114477 | 0.01 | 97236 | 98 | 0.01 | 0.08 | 0.05 | 0.08 |
53| 40.71 40.72 69.61 91.9 91.8 98.2 | 114057 | 0.01 | 97160 | 98 | 0.01 | 0.08 | 0.06 | 0.08 |
54| 40.57 40.74 69.54 92.0 91.7 98.1 | 113630 | 0 | 95124 | 96 | 0.04 | 0.08 | 0.03 | 0.08 |
55| 40.72 40.76 69.67 91.8 92.0 98.1 | 114337 | 0.01 | 96891 | 98 | 0.02 | 0.08 | 0.05 | 0.08 |
56| 40.61 40.69 69.61 91.9 91.9 98.1 | 113706 | 0 | 96398 | 97 | 0.02 | 0.08 | 0.05 | 0.08 |
57| 40.69 40.78 69.68 91.7 92.1 98.2 | 114295 | 0.01 | 94335 | 95 | 0.05 | 0.07 | 0.02 | 0.08 |
58| 40.69 40.72 69.61 91.8 91.9 97.8 | 114113 | 0.01 | 95856 | 97 | 0.03 | 0.08 | 0.05 | 0.09 |
59| 40.69 40.72 69.56 92.0 91.9 98.3 | 113930 | 0.01 | 96672 | 98 | 0.02 | 0.08 | 0.06 | 0.09 |
60| 40.69 40.78 69.52 91.9 91.9 98.2 | 114040 | 0.01 | 95933 | 97 | 0.03 | 0.08 | 0.05 | 0.09 |
61| 40.52 40.69 69.67 91.9 91.9 97.8 | 113655 | 0 | 96165 | 97 | 0.03 | 0.08 | 0.06 | 0.1 |
62| 40.71 40.75 69.54 92.0 91.9 98.2 | 114050 | 0.01 | 96188 | 97 | 0.03 | 0.08 | 0.06 | 0.1 |
63| 40.71 40.75 69.63 92.0 91.9 98.2 | 114206 | 0.01 | 97453 | 98 | 0.01 | 0.08 | 0.09 | 0.1 |
64| 40.69 40.78 69.58 91.9 91.9 98.2 | 114146 | 0.01 | 96828 | 98 | 0.02 | 0.08 | 0.12 | 0.14 |
65| 40.81 41.02 69.67 91.6 92.1 98.5 | 115183 | 0.02 | 93744 | 95 | 0.06 | 0.08 | 0.11 | 0.2 |
66| 40.37 40.76 69.67 91.8 91.6 98.3 | 113328 | 0 | 90262 | 91 | 0.12 | 0.08 | 0.19 | 0.31 |
67+----------------------------------+----------+----------------+------------+-------------+-------------------+-----------+-----------------+-----------------+
68Using d_min_step 0.1
69
70Indexed crystal models:
71model 1 (97056 reflections):
72Crystal:
73 Unit cell: 40.567, 40.760, 69.669, 91.778, 91.943, 98.463
74 Space group: P 1
75 U matrix: {{ 0.8416, 0.5366, 0.0607},
76 {-0.1829, 0.1774, 0.9670},
77 { 0.5082, -0.8250, 0.2474}}
78 B matrix: {{ 0.0247, 0.0000, 0.0000},
79 { 0.0037, 0.0248, 0.0000},
80 { 0.0010, 0.0009, 0.0144}}
81 A = UB: {{ 0.0228, 0.0134, 0.0009},
82 {-0.0029, 0.0053, 0.0139},
83 { 0.0097, -0.0202, 0.0036}}
84+------------+-------------+---------------+-------------+
85| Imageset | # indexed | # unindexed | % indexed |
86|------------+-------------+---------------+-------------|
87| 0 | 97056 | 2029 | 98 |
88+------------+-------------+---------------+-------------+
89
90################################################################################
91Starting refinement (macro-cycle 1)
92################################################################################
93
94
95Summary statistics for 96701 observations matched to predictions:
96+-------------------+--------+----------+----------+-----------+-------+
97| | Min | Q1 | Med | Q3 | Max |
98|-------------------+--------+----------+----------+-----------+-------|
99| Xc - Xo (mm) | -2.487 | -0.5688 | -0.09237 | 0.3731 | 1.997 |
100| Yc - Yo (mm) | -2.563 | -0.5829 | -0.2869 | -0.007452 | 4.035 |
101| Phic - Phio (deg) | -3.635 | -0.08989 | 0.0216 | 0.1372 | 4.669 |
102| X weights | 245.9 | 388.2 | 398.8 | 403.7 | 405.6 |
103| Y weights | 211.5 | 374 | 393.4 | 402.5 | 405.6 |
104| Phi weights | 40.59 | 47.93 | 48 | 48 | 48 |
105+-------------------+--------+----------+----------+-----------+-------+
106
107Detecting centroid outliers using the Tukey algorithm
1087237 reflections have been flagged as outliers
10989464 reflections remain in the manager
110
111Summary statistics for 89464 observations matched to predictions:
112+-------------------+---------+----------+---------+----------+--------+
113| | Min | Q1 | Med | Q3 | Max |
114|-------------------+---------+----------+---------+----------+--------|
115| Xc - Xo (mm) | -2.232 | -0.5527 | -0.0995 | 0.3616 | 1.997 |
116| Yc - Yo (mm) | -1.625 | -0.5842 | -0.2996 | -0.04293 | 1.016 |
117| Phic - Phio (deg) | -0.5249 | -0.08781 | 0.01698 | 0.124 | 0.5662 |
118| X weights | 246.4 | 388.9 | 399.1 | 403.8 | 405.6 |
119| Y weights | 211.5 | 374.5 | 393.8 | 402.6 | 405.6 |
120| Phi weights | 40.59 | 47.95 | 48 | 48 | 48 |
121+-------------------+---------+----------+---------+----------+--------+
122
123There are 16 parameters to refine against 36000 reflections in 3 dimensions
124
125Refinement steps:
126+--------+--------+----------+----------+------------+
127| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
128| | | (mm) | (mm) | (deg) |
129|--------+--------+----------+----------+------------|
130| 0 | 36000 | 0.6789 | 0.53255 | 0.15652 |
131| 1 | 36000 | 0.24932 | 0.26276 | 0.15022 |
132| 2 | 36000 | 0.10636 | 0.13773 | 0.13691 |
133| 3 | 36000 | 0.056622 | 0.062578 | 0.10997 |
134| 4 | 36000 | 0.051364 | 0.052926 | 0.10462 |
135| 5 | 36000 | 0.051099 | 0.052943 | 0.10458 |
136| 6 | 36000 | 0.051088 | 0.052952 | 0.10458 |
137| 7 | 36000 | 0.051088 | 0.052952 | 0.10458 |
138+--------+--------+----------+----------+------------+
139RMSD no longer decreasing
140
141RMSDs by experiment:
142+-------+--------+----------+----------+------------+
143| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
144| id | | (px) | (px) | (images) |
145|-------+--------+----------+----------+------------|
146| 0 | 36000 | 0.29702 | 0.30786 | 0.20917 |
147+-------+--------+----------+----------+------------+
148
149Refined crystal models:
150model 1 (97056 reflections):
151Crystal:
152 Unit cell: 40.5456(8), 40.5534(8), 69.2877(13), 92.0144(4), 91.9766(4), 98.0812(4)
153 Space group: P 1
154 U matrix: {{ 0.8429, 0.5343, 0.0638},
155 {-0.1841, 0.1750, 0.9672},
156 { 0.5056, -0.8270, 0.2459}}
157 B matrix: {{ 0.0247, 0.0000, 0.0000},
158 { 0.0035, 0.0249, 0.0000},
159 { 0.0010, 0.0010, 0.0145}}
160 A = UB: {{ 0.0227, 0.0134, 0.0009},
161 {-0.0030, 0.0053, 0.0140},
162 { 0.0098, -0.0203, 0.0036}}
163+------------+-------------+---------------+-------------+
164| Imageset | # indexed | # unindexed | % indexed |
165|------------+-------------+---------------+-------------|
166| 0 | 97056 | 2029 | 98 |
167+------------+-------------+---------------+-------------+
168Increasing resolution to 1.70 Angstrom
169
170Indexed crystal models:
171model 1 (105639 reflections):
172Crystal:
173 Unit cell: 40.5456(8), 40.5534(8), 69.2877(13), 92.0144(4), 91.9766(4), 98.0812(4)
174 Space group: P 1
175 U matrix: {{ 0.8429, 0.5343, 0.0638},
176 {-0.1841, 0.1750, 0.9672},
177 { 0.5056, -0.8270, 0.2459}}
178 B matrix: {{ 0.0247, 0.0000, 0.0000},
179 { 0.0035, 0.0249, 0.0000},
180 { 0.0010, 0.0010, 0.0145}}
181 A = UB: {{ 0.0227, 0.0134, 0.0009},
182 {-0.0030, 0.0053, 0.0140},
183 { 0.0098, -0.0203, 0.0036}}
184+------------+-------------+---------------+-------------+
185| Imageset | # indexed | # unindexed | % indexed |
186|------------+-------------+---------------+-------------|
187| 0 | 105848 | 431 | 99.6 |
188+------------+-------------+---------------+-------------+
189
190################################################################################
191Starting refinement (macro-cycle 2)
192################################################################################
193
194
195Summary statistics for 105281 observations matched to predictions:
196+-------------------+---------+----------+------------+---------+--------+
197| | Min | Q1 | Med | Q3 | Max |
198|-------------------+---------+----------+------------+---------+--------|
199| Xc - Xo (mm) | -0.3872 | -0.03715 | -0.003151 | 0.03167 | 0.3678 |
200| Yc - Yo (mm) | -0.9055 | -0.03122 | -0.0001547 | 0.03169 | 0.9764 |
201| Phic - Phio (deg) | -1.098 | -0.08155 | 0.001317 | 0.08361 | 0.9669 |
202| X weights | 241.2 | 384.7 | 397.6 | 403.4 | 405.6 |
203| Y weights | 173.8 | 369.2 | 391.1 | 402 | 405.6 |
204| Phi weights | 40.59 | 47.94 | 48 | 48 | 48 |
205+-------------------+---------+----------+------------+---------+--------+
206
207Detecting centroid outliers using the Tukey algorithm
2085530 reflections have been flagged as outliers
20999751 reflections remain in the manager
210
211Summary statistics for 99751 observations matched to predictions:
212+-------------------+---------+----------+------------+---------+--------+
213| | Min | Q1 | Med | Q3 | Max |
214|-------------------+---------+----------+------------+---------+--------|
215| Xc - Xo (mm) | -0.1729 | -0.03635 | -0.003496 | 0.03019 | 0.162 |
216| Yc - Yo (mm) | -0.1664 | -0.02973 | -0.0002873 | 0.02983 | 0.1935 |
217| Phic - Phio (deg) | -0.3506 | -0.08067 | 0.0007001 | 0.08181 | 0.3582 |
218| X weights | 241.2 | 386.4 | 398.2 | 403.6 | 405.6 |
219| Y weights | 206.6 | 371.9 | 392.3 | 402.2 | 405.6 |
220| Phi weights | 40.76 | 47.94 | 48 | 48 | 48 |
221+-------------------+---------+----------+------------+---------+--------+
222
223There are 16 parameters to refine against 36000 reflections in 3 dimensions
224
225Refinement steps:
226+--------+--------+----------+----------+------------+
227| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
228| | | (mm) | (mm) | (deg) |
229|--------+--------+----------+----------+------------|
230| 0 | 36000 | 0.048904 | 0.047004 | 0.10593 |
231| 1 | 36000 | 0.048644 | 0.046891 | 0.10558 |
232| 2 | 36000 | 0.048608 | 0.046908 | 0.10552 |
233| 3 | 36000 | 0.048598 | 0.046917 | 0.1055 |
234| 4 | 36000 | 0.048596 | 0.046919 | 0.1055 |
235+--------+--------+----------+----------+------------+
236RMSD no longer decreasing
237
238RMSDs by experiment:
239+-------+--------+----------+----------+------------+
240| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
241| id | | (px) | (px) | (images) |
242|-------+--------+----------+----------+------------|
243| 0 | 36000 | 0.28253 | 0.27278 | 0.211 |
244+-------+--------+----------+----------+------------+
245
246Refined crystal models:
247model 1 (105639 reflections):
248Crystal:
249 Unit cell: 40.5491(6), 40.5559(6), 69.2899(10), 92.0183(4), 91.9736(4), 98.0776(4)
250 Space group: P 1
251 U matrix: {{ 0.8429, 0.5343, 0.0638},
252 {-0.1841, 0.1749, 0.9672},
253 { 0.5056, -0.8270, 0.2458}}
254 B matrix: {{ 0.0247, 0.0000, 0.0000},
255 { 0.0035, 0.0249, 0.0000},
256 { 0.0010, 0.0010, 0.0145}}
257 A = UB: {{ 0.0227, 0.0134, 0.0009},
258 {-0.0030, 0.0053, 0.0140},
259 { 0.0098, -0.0203, 0.0036}}
260+------------+-------------+---------------+-------------+
261| Imageset | # indexed | # unindexed | % indexed |
262|------------+-------------+---------------+-------------|
263| 0 | 105639 | 640 | 99.4 |
264+------------+-------------+---------------+-------------+
265Increasing resolution to 1.57 Angstrom
266
267Indexed crystal models:
268model 1 (109664 reflections):
269Crystal:
270 Unit cell: 40.5491(6), 40.5559(6), 69.2899(10), 92.0183(4), 91.9736(4), 98.0776(4)
271 Space group: P 1
272 U matrix: {{ 0.8429, 0.5343, 0.0638},
273 {-0.1841, 0.1749, 0.9672},
274 { 0.5056, -0.8270, 0.2458}}
275 B matrix: {{ 0.0247, 0.0000, 0.0000},
276 { 0.0035, 0.0249, 0.0000},
277 { 0.0010, 0.0010, 0.0145}}
278 A = UB: {{ 0.0227, 0.0134, 0.0009},
279 {-0.0030, 0.0053, 0.0140},
280 { 0.0098, -0.0203, 0.0036}}
281+------------+-------------+---------------+-------------+
282| Imageset | # indexed | # unindexed | % indexed |
283|------------+-------------+---------------+-------------|
284| 0 | 109674 | 722 | 99.3 |
285+------------+-------------+---------------+-------------+
286
287################################################################################
288Starting refinement (macro-cycle 3)
289################################################################################
290
291
292Summary statistics for 109289 observations matched to predictions:
293+-------------------+---------+----------+------------+---------+--------+
294| | Min | Q1 | Med | Q3 | Max |
295|-------------------+---------+----------+------------+---------+--------|
296| Xc - Xo (mm) | -0.3857 | -0.03609 | -0.001334 | 0.0331 | 0.3619 |
297| Yc - Yo (mm) | -1.202 | -0.03314 | -0.0008305 | 0.0316 | 1.496 |
298| Phic - Phio (deg) | -1.052 | -0.08187 | 0.0009273 | 0.08412 | 1.135 |
299| X weights | 210.4 | 382.7 | 397 | 403.3 | 405.6 |
300| Y weights | 173.8 | 366.5 | 389.9 | 401.7 | 405.6 |
301| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
302+-------------------+---------+----------+------------+---------+--------+
303
304Detecting centroid outliers using the Tukey algorithm
3055980 reflections have been flagged as outliers
306103309 reflections remain in the manager
307
308Summary statistics for 103309 observations matched to predictions:
309+-------------------+---------+----------+------------+---------+--------+
310| | Min | Q1 | Med | Q3 | Max |
311|-------------------+---------+----------+------------+---------+--------|
312| Xc - Xo (mm) | -0.1753 | -0.03502 | -0.001402 | 0.03179 | 0.1659 |
313| Yc - Yo (mm) | -0.173 | -0.03133 | -0.0008288 | 0.02984 | 0.1995 |
314| Phic - Phio (deg) | -0.3661 | -0.08094 | 0.0004713 | 0.08242 | 0.3457 |
315| X weights | 210.9 | 384.7 | 397.7 | 403.4 | 405.6 |
316| Y weights | 204 | 369.5 | 391.3 | 402 | 405.6 |
317| Phi weights | 39.29 | 47.94 | 48 | 48 | 48 |
318+-------------------+---------+----------+------------+---------+--------+
319
320There are 16 parameters to refine against 36000 reflections in 3 dimensions
321
322Refinement steps:
323+--------+--------+----------+----------+------------+
324| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
325| | | (mm) | (mm) | (deg) |
326|--------+--------+----------+----------+------------|
327| 0 | 36000 | 0.04896 | 0.048335 | 0.10627 |
328| 1 | 36000 | 0.048925 | 0.048264 | 0.10615 |
329| 2 | 36000 | 0.048919 | 0.048237 | 0.10616 |
330| 3 | 36000 | 0.048921 | 0.048222 | 0.10618 |
331| 4 | 36000 | 0.048923 | 0.048219 | 0.10618 |
332+--------+--------+----------+----------+------------+
333RMSD no longer decreasing
334
335RMSDs by experiment:
336+-------+--------+----------+----------+------------+
337| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
338| id | | (px) | (px) | (images) |
339|-------+--------+----------+----------+------------|
340| 0 | 36000 | 0.28444 | 0.28034 | 0.21236 |
341+-------+--------+----------+----------+------------+
342
343Refined crystal models:
344model 1 (109664 reflections):
345Crystal:
346 Unit cell: 40.5500(5), 40.5565(5), 69.2900(9), 92.0192(3), 91.9731(3), 98.0756(4)
347 Space group: P 1
348 U matrix: {{ 0.8429, 0.5343, 0.0638},
349 {-0.1841, 0.1749, 0.9672},
350 { 0.5056, -0.8270, 0.2458}}
351 B matrix: {{ 0.0247, 0.0000, 0.0000},
352 { 0.0035, 0.0249, 0.0000},
353 { 0.0010, 0.0010, 0.0145}}
354 A = UB: {{ 0.0227, 0.0134, 0.0009},
355 {-0.0030, 0.0053, 0.0140},
356 { 0.0098, -0.0203, 0.0036}}
357+------------+-------------+---------------+-------------+
358| Imageset | # indexed | # unindexed | % indexed |
359|------------+-------------+---------------+-------------|
360| 0 | 109664 | 732 | 99.3 |
361+------------+-------------+---------------+-------------+
362Increasing resolution to 1.43 Angstrom
363
364Indexed crystal models:
365model 1 (111070 reflections):
366Crystal:
367 Unit cell: 40.5500(5), 40.5565(5), 69.2900(9), 92.0192(3), 91.9731(3), 98.0756(4)
368 Space group: P 1
369 U matrix: {{ 0.8429, 0.5343, 0.0638},
370 {-0.1841, 0.1749, 0.9672},
371 { 0.5056, -0.8270, 0.2458}}
372 B matrix: {{ 0.0247, 0.0000, 0.0000},
373 { 0.0035, 0.0249, 0.0000},
374 { 0.0010, 0.0010, 0.0145}}
375 A = UB: {{ 0.0227, 0.0134, 0.0009},
376 {-0.0030, 0.0053, 0.0140},
377 { 0.0098, -0.0203, 0.0036}}
378+------------+-------------+---------------+-------------+
379| Imageset | # indexed | # unindexed | % indexed |
380|------------+-------------+---------------+-------------|
381| 0 | 111081 | 755 | 99.3 |
382+------------+-------------+---------------+-------------+
383
384################################################################################
385Starting refinement (macro-cycle 4)
386################################################################################
387
388
389Summary statistics for 110691 observations matched to predictions:
390+-------------------+--------+----------+------------+---------+--------+
391| | Min | Q1 | Med | Q3 | Max |
392|-------------------+--------+----------+------------+---------+--------|
393| Xc - Xo (mm) | -1.938 | -0.0358 | -0.0005585 | 0.03385 | 0.3621 |
394| Yc - Yo (mm) | -1.139 | -0.03288 | -0.0002335 | 0.03253 | 1.509 |
395| Phic - Phio (deg) | -1.054 | -0.08176 | 0.001372 | 0.08471 | 1.147 |
396| X weights | 210.4 | 381.9 | 396.8 | 403.2 | 405.6 |
397| Y weights | 173.5 | 365.3 | 389.4 | 401.6 | 405.6 |
398| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
399+-------------------+--------+----------+------------+---------+--------+
400
401Detecting centroid outliers using the Tukey algorithm
4026118 reflections have been flagged as outliers
403104573 reflections remain in the manager
404
405Summary statistics for 104573 observations matched to predictions:
406+-------------------+---------+----------+------------+---------+--------+
407| | Min | Q1 | Med | Q3 | Max |
408|-------------------+---------+----------+------------+---------+--------|
409| Xc - Xo (mm) | -0.1744 | -0.03479 | -0.0006967 | 0.03248 | 0.1659 |
410| Yc - Yo (mm) | -0.1723 | -0.03094 | -0.0002347 | 0.03068 | 0.2011 |
411| Phic - Phio (deg) | -0.3504 | -0.0807 | 0.0009259 | 0.08309 | 0.3515 |
412| X weights | 210.9 | 384 | 397.6 | 403.4 | 405.6 |
413| Y weights | 191.7 | 368.6 | 390.9 | 401.9 | 405.6 |
414| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
415+-------------------+---------+----------+------------+---------+--------+
416
417There are 16 parameters to refine against 36000 reflections in 3 dimensions
418
419Refinement steps:
420+--------+--------+----------+----------+------------+
421| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
422| | | (mm) | (mm) | (deg) |
423|--------+--------+----------+----------+------------|
424| 0 | 36000 | 0.049346 | 0.048752 | 0.10663 |
425| 1 | 36000 | 0.049345 | 0.048728 | 0.10659 |
426| 2 | 36000 | 0.049346 | 0.048716 | 0.10659 |
427| 3 | 36000 | 0.049348 | 0.048709 | 0.1066 |
428| 4 | 36000 | 0.049349 | 0.048707 | 0.1066 |
429+--------+--------+----------+----------+------------+
430RMSD no longer decreasing
431
432RMSDs by experiment:
433+-------+--------+----------+----------+------------+
434| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
435| id | | (px) | (px) | (images) |
436|-------+--------+----------+----------+------------|
437| 0 | 36000 | 0.28691 | 0.28318 | 0.21321 |
438+-------+--------+----------+----------+------------+
439
440Refined crystal models:
441model 1 (111070 reflections):
442Crystal:
443 Unit cell: 40.5508(5), 40.5576(5), 69.2906(8), 92.0192(3), 91.9721(3), 98.0758(4)
444 Space group: P 1
445 U matrix: {{ 0.8429, 0.5343, 0.0638},
446 {-0.1841, 0.1749, 0.9672},
447 { 0.5056, -0.8270, 0.2458}}
448 B matrix: {{ 0.0247, 0.0000, 0.0000},
449 { 0.0035, 0.0249, 0.0000},
450 { 0.0010, 0.0010, 0.0145}}
451 A = UB: {{ 0.0227, 0.0134, 0.0009},
452 {-0.0030, 0.0053, 0.0140},
453 { 0.0098, -0.0203, 0.0036}}
454+------------+-------------+---------------+-------------+
455| Imageset | # indexed | # unindexed | % indexed |
456|------------+-------------+---------------+-------------|
457| 0 | 111070 | 766 | 99.3 |
458+------------+-------------+---------------+-------------+
459Increasing resolution to 1.29 Angstrom
460
461Indexed crystal models:
462model 1 (111252 reflections):
463Crystal:
464 Unit cell: 40.5508(5), 40.5576(5), 69.2906(8), 92.0192(3), 91.9721(3), 98.0758(4)
465 Space group: P 1
466 U matrix: {{ 0.8429, 0.5343, 0.0638},
467 {-0.1841, 0.1749, 0.9672},
468 { 0.5056, -0.8270, 0.2458}}
469 B matrix: {{ 0.0247, 0.0000, 0.0000},
470 { 0.0035, 0.0249, 0.0000},
471 { 0.0010, 0.0010, 0.0145}}
472 A = UB: {{ 0.0227, 0.0134, 0.0009},
473 {-0.0030, 0.0053, 0.0140},
474 { 0.0098, -0.0203, 0.0036}}
475+------------+-------------+---------------+-------------+
476| Imageset | # indexed | # unindexed | % indexed |
477|------------+-------------+---------------+-------------|
478| 0 | 111265 | 756 | 99.3 |
479+------------+-------------+---------------+-------------+
480
481################################################################################
482Starting refinement (macro-cycle 5)
483################################################################################
484
485
486Summary statistics for 110874 observations matched to predictions:
487+-------------------+--------+----------+------------+---------+--------+
488| | Min | Q1 | Med | Q3 | Max |
489|-------------------+--------+----------+------------+---------+--------|
490| Xc - Xo (mm) | -1.936 | -0.03546 | -5.793e-05 | 0.03441 | 0.3642 |
491| Yc - Yo (mm) | -1.105 | -0.03305 | -0.0002103 | 0.03258 | 1.504 |
492| Phic - Phio (deg) | -1.06 | -0.08184 | 0.001222 | 0.08479 | 1.144 |
493| X weights | 210.4 | 381.8 | 396.8 | 403.2 | 405.6 |
494| Y weights | 143.8 | 365.2 | 389.4 | 401.6 | 405.6 |
495| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
496+-------------------+--------+----------+------------+---------+--------+
497
498Detecting centroid outliers using the Tukey algorithm
4996119 reflections have been flagged as outliers
500104755 reflections remain in the manager
501
502Summary statistics for 104755 observations matched to predictions:
503+-------------------+---------+----------+------------+---------+--------+
504| | Min | Q1 | Med | Q3 | Max |
505|-------------------+---------+----------+------------+---------+--------|
506| Xc - Xo (mm) | -0.1728 | -0.0345 | -0.000241 | 0.03305 | 0.1644 |
507| Yc - Yo (mm) | -0.1713 | -0.03113 | -0.0002322 | 0.0306 | 0.2007 |
508| Phic - Phio (deg) | -0.3465 | -0.08074 | 0.0008338 | 0.08306 | 0.3513 |
509| X weights | 210.9 | 383.9 | 397.5 | 403.4 | 405.6 |
510| Y weights | 143.8 | 368.5 | 390.9 | 401.9 | 405.6 |
511| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
512+-------------------+---------+----------+------------+---------+--------+
513
514There are 16 parameters to refine against 36000 reflections in 3 dimensions
515
516Refinement steps:
517+--------+--------+----------+----------+------------+
518| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
519| | | (mm) | (mm) | (deg) |
520|--------+--------+----------+----------+------------|
521| 0 | 36000 | 0.049652 | 0.049203 | 0.10673 |
522| 1 | 36000 | 0.049613 | 0.049223 | 0.10673 |
523| 2 | 36000 | 0.049602 | 0.049229 | 0.10674 |
524| 3 | 36000 | 0.049601 | 0.049228 | 0.10674 |
525+--------+--------+----------+----------+------------+
526RMSD no longer decreasing
527
528RMSDs by experiment:
529+-------+--------+----------+----------+------------+
530| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
531| id | | (px) | (px) | (images) |
532|-------+--------+----------+----------+------------|
533| 0 | 36000 | 0.28838 | 0.28621 | 0.21348 |
534+-------+--------+----------+----------+------------+
535
536Refined crystal models:
537model 1 (111252 reflections):
538Crystal:
539 Unit cell: 40.5513(5), 40.5578(5), 69.2911(8), 92.0192(3), 91.9720(3), 98.0758(4)
540 Space group: P 1
541 U matrix: {{ 0.8429, 0.5343, 0.0638},
542 {-0.1841, 0.1749, 0.9672},
543 { 0.5056, -0.8270, 0.2458}}
544 B matrix: {{ 0.0247, 0.0000, 0.0000},
545 { 0.0035, 0.0249, 0.0000},
546 { 0.0010, 0.0010, 0.0145}}
547 A = UB: {{ 0.0227, 0.0134, 0.0009},
548 {-0.0030, 0.0053, 0.0140},
549 { 0.0098, -0.0203, 0.0036}}
550+------------+-------------+---------------+-------------+
551| Imageset | # indexed | # unindexed | % indexed |
552|------------+-------------+---------------+-------------|
553| 0 | 111252 | 769 | 99.3 |
554+------------+-------------+---------------+-------------+
555Saving refined experiments to indexed.expt
556Saving refined reflections to indexed.refl
If successful, dials.index writes two output data files - an
indexed.expt containing the tuned
experimental model and determined parameters, and a indexed.refl
reflection file, including index data from the best fit.
It is worth reading through this output to understand what the indexing
program has done. Note that this log is automatically captured in the file
dials.index.log. A more verbose debug log can be generated by adding
the ‘-v’ option to a dials command line program, but this is probably only
helpful if something has gone wrong and you are trying to track down why.
Inspecting the beginning of the log shows that the indexing step is done at a resolution lower than the full dataset; 1.84 Å:
9Found max_cell: 94.4 Angstrom
10Setting d_min: 1.84
11FFT gridding: (256,256,256)
The resolution limit of data that can be used in indexing is determined by the size of the 3D FFT grid, and the likely maximum cell dimension. Here we used the default 256³ grid points. These are used to make an initial estimate for the unit cell parameters.
What then follows are ‘macro-cycles’ of refinement where the experimental model is first tuned to get the best possible fit from the data, and then the resolution limit is reduced to cover more data than the previous cycle. 16 parameters of the diffraction geometry are tuned - 6 for the detector, one for beam angle, 3 crystal orientation angles and the 6 triclinic cell parameters. At each stage only 36000 reflections are used in the refinement job. In order to save time, a subset of the input reflections are used - by default using 100 reflections for every degree of the 360° scan.
We see that the first macrocycle of refinement makes a big improvement in the positional RMSDs:
126+--------+--------+----------+----------+------------+
127| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
128| | | (mm) | (mm) | (deg) |
129|--------+--------+----------+----------+------------|
130| 0 | 36000 | 0.6789 | 0.53255 | 0.15652 |
131| 1 | 36000 | 0.24932 | 0.26276 | 0.15022 |
132| 2 | 36000 | 0.10636 | 0.13773 | 0.13691 |
133| 3 | 36000 | 0.056622 | 0.062578 | 0.10997 |
134| 4 | 36000 | 0.051364 | 0.052926 | 0.10462 |
135| 5 | 36000 | 0.051099 | 0.052943 | 0.10458 |
136| 6 | 36000 | 0.051088 | 0.052952 | 0.10458 |
137| 7 | 36000 | 0.051088 | 0.052952 | 0.10458 |
138+--------+--------+----------+----------+------------+
Second and subsequent macrocycles are refined using the same number of reflections, but after extending to higher resolution. The RMSDs at the start of each cycle start off worse than at the end of the previous cycle, because the best fit model for lower resolution data is being applied to higher resolution reflections. As long as each macrocyle shows a reduction in RMSDs then refinement is doing its job of extending the applicability of the model out to a new resolution limit, until eventually the highest resolution strong spots have been included. The final macrocycle includes data out to 1.30 Å and produces a final model with RMSDs of 0.050 mm in X, 0.049 mm in Y and 0.104° in φ, corresponding to 0.29 pixels in X, 0.28 pixels in Y and 0.21 image widths in φ.
Despite the high quality of this data, we notice from the log that at each macrocycle there were some outliers identified and removed from refinement as resolution increases. Large outliers can dominate refinement using a least squares target, so it is important to be able to remove these. More about this is discussed below in Refinement. It’s also worth checking the total number of reflections that were unable to be assigned an index:
550+------------+-------------+---------------+-------------+
551| Imageset | # indexed | # unindexed | % indexed |
552|------------+-------------+---------------+-------------|
553| 0 | 111252 | 769 | 99.3 |
554+------------+-------------+---------------+-------------+
because this can be an indication of poor data quality or a sign that more
care needs to be taken in selecting the strategy used by dials.index.
After indexing it can be useful to inspect the reciprocal lattice again:
dials.reciprocal_lattice_viewer indexed.expt indexed.refl
Now indexed/unindexed spots are differentiated by colour, and it is possible to see which spots were marked by dials.refine as outliers. If you have a dataset with multiple lattices present, it may be possible to spot them in the unindexed reflections.
In this case, we can see that the refinement has clearly resolved whatever systematic error was causing distortions in the reciprocal space view, and the determined reciprocal unit cell fits the data well:
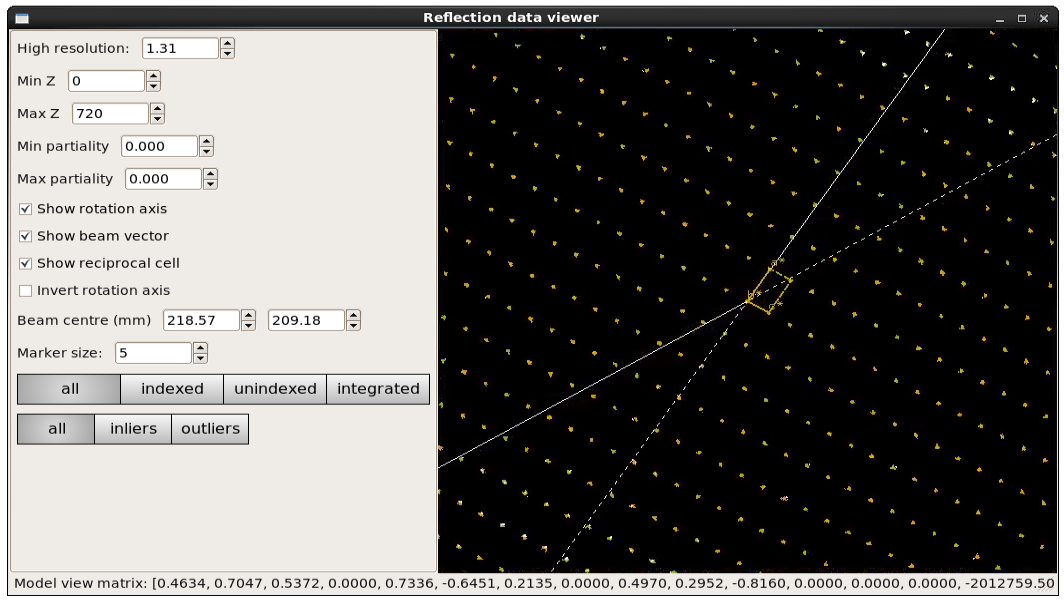
Bravais Lattice Refinement¶
Since we didn’t know the Bravais lattice before indexing, we can now use dials.refine_bravais_settings to determine likely candidates. This takes the results of the P1 autoindexing and runs refinement with all of the possible Bravais settings applied, allowing you to choose your preferred solution:
dials.refine_bravais_settings indexed.expt indexed.refl
giving a table containing scoring data and unit cell for each Bravais setting:
Chiral space groups corresponding to each Bravais lattice:
aP: P1
mP: P2 P21
mC: C2
oC: C2221 C222
+------------+--------------+--------+--------------+----------+-----------+------------------------------------------+----------+------------+
| Solution | Metric fit | rmsd | min/max cc | #spots | lattice | unit_cell | volume | cb_op |
|------------+--------------+--------+--------------+----------+-----------+------------------------------------------+----------+------------|
| 5 | 3.0451 | 2.311 | 0.583/0.982 | 30319 | oC | 52.56 60.59 68.39 90.00 90.00 90.00 | 217763 | a+b,-a+b,c |
| 4 | 3.045 | 2.312 | 0.590/0.590 | 30299 | mC | 60.61 52.57 68.41 90.00 89.91 90.00 | 217975 | a-b,a+b,c |
| 3 | 3.0451 | 2.311 | 0.583/0.583 | 30327 | mP | 40.11 68.39 40.10 90.00 98.12 90.00 | 108888 | -a,-c,-b |
| * 2 | 0.0323 | 0.071 | 0.982/0.982 | 35478 | mC | 53.17 61.25 69.29 90.00 93.05 90.00 | 225327 | a+b,-a+b,c |
| * 1 | 0 | 0.069 | -/- | 35669 | aP | 40.55 40.56 69.29 92.02 91.97 98.08 | 112674 | a,b,c |
+------------+--------------+--------+--------------+----------+-----------+------------------------------------------+----------+------------+
* = recommended solution
Saving summary as bravais_summary.json
Saving solution 5 as bravais_setting_5.expt
Saving solution 4 as bravais_setting_4.expt
Saving solution 3 as bravais_setting_3.expt
Saving solution 2 as bravais_setting_2.expt
Saving solution 1 as bravais_setting_1.expt
The scores include the metric fit (in degrees), RMSDs (in mm), and the best and worse correlation coefficients for data related by symmetry elements implied by the lowest symmetry space group from the Bravais setting. This uses the raw spot intensity measurement from the spot- finding procedure (uncorrected and unscaled) but provides a very useful check to see if the data does appear to adhere to the proposed symmetry operators.
A separate bravais_setting_N.expt experiments file is written for
each plausible lattice type, corresponding to the solution index. In this
example we choose to continue processing with
bravais_setting_2.expt, which is the highest symmetry suggested
result - the options 3, 4, 5 have higher symmetries, but at the cost of
a steep jump in RMSd’s and worsening of fit.
In cases where the change of basis operator to the chosen setting is the
identity operator (a,b,c) we can proceed directly to further
refinement. However, we notice that the change of basis operator for our
chosen solution is a+b,-a+b,c, so it is necessary to reindex the
indexed.refl file output by using
dials.reindex:
dials.reindex indexed.refl change_of_basis_op=a+b,-a+b,c
This outputs the file reindexed.refl which we now
use as input to downstream programs, in place of the original
indexed.refl.
Refinement¶
The model is already refined during indexing, but we can also add explicit
refinement steps using dials.refine
in here, to use all reflections in refinement rather than a subset and to
fit a scan-varying model of the crystal. There are many options to
refinement - to show all the options up to and including expert_level=1
use this command:
dials.refine -c -e 1
and descriptions of each of the options can be included by adding -a1 to
the command. All of the main DIALS tools have equivalent command-line options
to list available options.
To refine over all reflections, and include the monoclinic constraints
from dials.refine_bravais_settings run:
dials.refine bravais_setting_2.expt reindexed.refl
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3
4input {
5 experiments = bravais_setting_2.expt
6 reflections = reindexed.refl
7}
8
9Configuring refiner
10Setting outlier.nproc=32
11
12Summary statistics for 110874 observations matched to predictions:
13+-------------------+--------+----------+------------+---------+--------+
14| | Min | Q1 | Med | Q3 | Max |
15|-------------------+--------+----------+------------+---------+--------|
16| Xc - Xo (mm) | -1.947 | -0.03566 | -0.0004947 | 0.0338 | 0.3564 |
17| Yc - Yo (mm) | -1.168 | -0.03535 | -0.0004064 | 0.03439 | 1.693 |
18| Phic - Phio (deg) | -1.089 | -0.08303 | 0.0007592 | 0.0842 | 1.274 |
19| X weights | 210.4 | 381.8 | 396.8 | 403.2 | 405.6 |
20| Y weights | 143.8 | 365.2 | 389.4 | 401.6 | 405.6 |
21| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
22+-------------------+--------+----------+------------+---------+--------+
23
24Detecting centroid outliers using the MCD algorithm
2511910 reflections have been flagged as outliers
2698964 reflections remain in the manager
27
28Summary statistics for 98964 observations matched to predictions:
29+-------------------+---------+----------+------------+---------+--------+
30| | Min | Q1 | Med | Q3 | Max |
31|-------------------+---------+----------+------------+---------+--------|
32| Xc - Xo (mm) | -0.1759 | -0.03443 | -0.001516 | 0.02988 | 0.1689 |
33| Yc - Yo (mm) | -0.1959 | -0.03195 | -0.0008095 | 0.02984 | 0.2338 |
34| Phic - Phio (deg) | -0.3644 | -0.07963 | 0.0006416 | 0.08122 | 0.3332 |
35| X weights | 210.9 | 385.4 | 398.1 | 403.6 | 405.6 |
36| Y weights | 143.8 | 370.7 | 392.1 | 402.2 | 405.6 |
37| Phi weights | 40.76 | 47.94 | 48 | 48 | 48 |
38+-------------------+---------+----------+------------+---------+--------+
39
40There are 14 parameters to refine against 98964 reflections in 3 dimensions
41Performing refinement of a single Experiment...
42
43Refinement steps:
44+--------+--------+----------+----------+------------+
45| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
46| | | (mm) | (mm) | (deg) |
47|--------+--------+----------+----------+------------|
48| 0 | 98964 | 0.046464 | 0.04815 | 0.10464 |
49| 1 | 98964 | 0.0464 | 0.04805 | 0.10467 |
50| 2 | 98964 | 0.046384 | 0.048019 | 0.10472 |
51| 3 | 98964 | 0.046389 | 0.048006 | 0.10474 |
52| 4 | 98964 | 0.046393 | 0.048001 | 0.10475 |
53+--------+--------+----------+----------+------------+
54RMSD no longer decreasing
55
56RMSDs by experiment:
57+-------+--------+----------+----------+------------+
58| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
59| id | | (px) | (px) | (images) |
60|-------+--------+----------+----------+------------|
61| 0 | 98964 | 0.26972 | 0.27907 | 0.20949 |
62+-------+--------+----------+----------+------------+
63Updating predictions for indexed reflections
64
65Scan-varying refinement
66Configuring refiner
67
68Summary statistics for 110871 observations matched to predictions:
69+-------------------+--------+----------+------------+---------+--------+
70| | Min | Q1 | Med | Q3 | Max |
71|-------------------+--------+----------+------------+---------+--------|
72| Xc - Xo (mm) | -1.939 | -0.03434 | 0.0006411 | 0.03494 | 0.3636 |
73| Yc - Yo (mm) | -1.178 | -0.03519 | -9.027e-05 | 0.03468 | 1.732 |
74| Phic - Phio (deg) | -1.058 | -0.08385 | 0.0001672 | 0.08374 | 1.3 |
75| X weights | 210.4 | 381.8 | 396.8 | 403.2 | 405.6 |
76| Y weights | 143.8 | 365.2 | 389.4 | 401.6 | 405.6 |
77| Phi weights | 39.29 | 47.95 | 48 | 48 | 48 |
78+-------------------+--------+----------+------------+---------+--------+
79
80Detecting centroid outliers using the MCD algorithm
8112123 reflections have been flagged as outliers
8298748 reflections remain in the manager
83
84Summary statistics for 98748 observations matched to predictions:
85+-------------------+---------+----------+------------+---------+--------+
86| | Min | Q1 | Med | Q3 | Max |
87|-------------------+---------+----------+------------+---------+--------|
88| Xc - Xo (mm) | -0.1762 | -0.03299 | -0.0004204 | 0.0307 | 0.1751 |
89| Yc - Yo (mm) | -0.1849 | -0.03158 | -0.0003396 | 0.03044 | 0.265 |
90| Phic - Phio (deg) | -0.3683 | -0.08056 | 4.66e-05 | 0.08058 | 0.3418 |
91| X weights | 210.9 | 385.5 | 398.2 | 403.6 | 405.6 |
92| Y weights | 143.8 | 370.7 | 392.1 | 402.3 | 405.6 |
93| Phi weights | 40.76 | 47.94 | 48 | 48 | 48 |
94+-------------------+---------+----------+------------+---------+--------+
95
96There are 91 parameters to refine against 98748 reflections in 3 dimensions
97Performing refinement of a single Experiment...
98
99Refinement steps:
100+--------+--------+----------+----------+------------+
101| Step | Nref | RMSD_X | RMSD_Y | RMSD_Phi |
102| | | (mm) | (mm) | (deg) |
103|--------+--------+----------+----------+------------|
104| 0 | 98748 | 0.046156 | 0.047968 | 0.10469 |
105| 1 | 98748 | 0.043284 | 0.040801 | 0.10336 |
106| 2 | 98748 | 0.041282 | 0.039834 | 0.10273 |
107| 3 | 98748 | 0.040736 | 0.03963 | 0.10239 |
108| 4 | 98748 | 0.040622 | 0.03962 | 0.10218 |
109| 5 | 98748 | 0.040599 | 0.039617 | 0.10207 |
110| 6 | 98748 | 0.040595 | 0.039616 | 0.10205 |
111| 7 | 98748 | 0.040593 | 0.039617 | 0.10205 |
112+--------+--------+----------+----------+------------+
113RMSD no longer decreasing
114
115RMSDs by experiment:
116+-------+--------+----------+----------+------------+
117| Exp | Nref | RMSD_X | RMSD_Y | RMSD_Z |
118| id | | (px) | (px) | (images) |
119|-------+--------+----------+----------+------------|
120| 0 | 98748 | 0.23601 | 0.23033 | 0.2041 |
121+-------+--------+----------+----------+------------+
122Updating predictions for indexed reflections
123
124Final refined crystal model:
125Crystal:
126 Unit cell: 53.1694(3), 61.2423(5), 69.2879(5), 90.0, 93.04523(17), 90.0
127 Space group: C 1 2 1
128 U matrix: {{ 0.9560, -0.2863, 0.0639},
129 { 0.0114, 0.2539, 0.9672},
130 {-0.2931, -0.9239, 0.2460}}
131 B matrix: {{ 0.0188, 0.0000, 0.0000},
132 {-0.0000, 0.0163, 0.0000},
133 { 0.0010, 0.0000, 0.0145}}
134 A = UB: {{ 0.0180, -0.0047, 0.0009},
135 { 0.0012, 0.0041, 0.0140},
136 {-0.0053, -0.0151, 0.0036}}
137 A sampled at 721 scan points
138Saving refined experiments to refined.expt
139Saving reflections with updated predictions to refined.refl
This provides a good reduction in RMSDs, indicating a better fit, and writes
the results out to refined.expt and refined.refl.
Two passes of refinement are actually done here - an initial pass where unit cell and crystal rotation is consistent over the length of the experiment, and a second pass where these are allowed to vary. This scan-varying refinement allows compensation for small missets in the rotation of the goniometer, and compensation for changes to the unit cell dimensions; typically due to radiation damage. By default, the refinement looks for smooth changes over intervals of 30°, to avoid fitting unphysical models to noise, though this interval can be configured.
We can use the HTML report, described shortly, to view the results of fitting to smoothly varying crystal cell parameters:
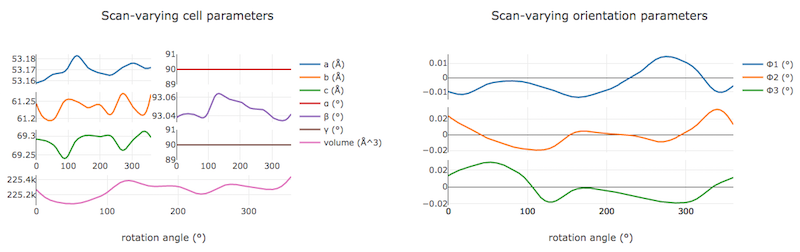
In this tutorial, we see no overall increase in all three cell parameters. If significant cell volume increases had been observed that might be indicative of radiation damage. However we can’t yet conclude that there is no radiation damage from the lack of considerable change observed.
Integration¶
After the refinement is done the next step is integration, which is performed by the program dials.integrate. Mostly, the default parameters are fine for Pilatus data, which will perform XDS-like 3D profile fitting while using a generalized linear model in order to fit a Poisson-distributed background model. We will also increase the number of processors used to speed the job up.
dials.integrate refined.expt refined.refl nproc=4
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3integration {
4 mp {
5 nproc = 4
6 }
7}
8input {
9 experiments = refined.expt
10 reflections = refined.refl
11}
12
13
14================================================================================
15
16Experiments
17
18Models for experiment 0
19
20Beam:
21 probe: x-ray
22 wavelength: 1.23985
23 sample to source direction : {0.000837355,-0,1}
24 divergence: 0
25 sigma divergence: 0
26 polarization normal: {0,1,0}
27 polarization fraction: 0.999
28 flux: 0
29 transmission: 1
30 sample to source distance: 0
31
32Detector:
33Panel:
34 name: Panel
35 type: SENSOR_PAD
36 identifier:
37 pixel_size:{0.172,0.172}
38 image_size: {2463,2527}
39 trusted_range: {0,1.22424e+06}
40 thickness: 0.32
41 material: Si
42 mu: 7.89652
43 gain: 1
44 pedestal: 0
45 fast_axis: {0.999913,-0.0055633,-0.011934}
46 slow_axis: {-0.0056763,-0.999939,-0.00945575}
47 origin: {-217.506,210.384,-164.52}
48 distance: 169.088
49 pixel to millimeter strategy: ParallaxCorrectedPxMmStrategy
50 mu: 7.89652
51 t0: 0.32
52
53Goniometer:
54 Rotation axis: {1,0,0}
55 Fixed rotation: {0.965028,0.0598562,-0.255222,-0.128604,-0.74028,-0.659883,-0.228434,0.669628,-0.706694}
56 Setting rotation:{1,0,0,0,1,0,0,0,1}
57 Axis #0 (GON_PHI): {1,0,0}
58 Axis #1 (GON_KAPPA): {0.914,0.279,-0.297}
59 Axis #2 (GON_OMEGA): {1,0,0}
60 Angles: 102.6,37.9,0
61 scan axis: #2 (GON_OMEGA)
62
63Scan:
64 number of images: 720
65 image range: {1,720}
66 epoch: 1.46307e+09
67 exposure time: 0.5
68 oscillation: {0,0.5}
69
70Crystal:
71 Unit cell: 53.1694(3), 61.2423(5), 69.2879(5), 90.0, 93.04523(17), 90.0
72 Space group: C 1 2 1
73 U matrix: {{ 0.9560, -0.2863, 0.0639},
74 { 0.0114, 0.2539, 0.9672},
75 {-0.2931, -0.9239, 0.2460}}
76 B matrix: {{ 0.0188, 0.0000, 0.0000},
77 {-0.0000, 0.0163, 0.0000},
78 { 0.0010, 0.0000, 0.0145}}
79 A = UB: {{ 0.0180, -0.0047, 0.0009},
80 { 0.0012, 0.0041, 0.0140},
81 {-0.0053, -0.0151, 0.0036}}
82 A sampled at 721 scan points
83
84================================================================================
85
86Initialising
87Processing reference reflections
88 read 112023 strong spots
89 removing 771 unindexed reflections
90 removing 12505 reflections marked as bad for refinement
91 using 98747 indexed reflections
92 found 13276 junk reflections
93 masked neighbouring pixels in 5 shoeboxes
94
95================================================================================
96
97Predicting reflections
98Prediction type: scan varying crystal prediction
99Predicted 368589 reflections
100Matching reference spots with predicted reflections
101 98747 observed reflections input
102 368589 reflections predicted
103 98747 reflections matched
104 98747 reflections accepted
105Using 98746 / 98747 reflections for sigma calculation
106Calculating E.S.D Beam Divergence.
107Calculating E.S.D Reflecting Range (mosaicity).
108 sigma b: 0.044239 degrees
109 sigma m: 0.057673 degrees
110================================================================================
111
112Processing reflections
113
114 Processing the following experiments:
115
116 Experiments: 1
117 Beams: 1
118 Detectors: 1
119 Goniometers: 1
120 Scans: 1
121 Crystals: 1
122 Imagesets: 1
123
124================================================================================
125
126Modelling reflection profiles
127
128 Split 13 reflections overlapping job boundaries
129
130Memory situation report:
131 Available system memory : 201.2 GB
132 Maximum memory for processing : 181.1 GB
133 Memory required per process : 0.0 GB
134
135Processing reflections in the following blocks of images:
136
137 block_size: Auto
138
139+-----+---------+--------------+------------+--------------+------------+-----------------+
140| # | Group | Frame From | Frame To | Angle From | Angle To | # Reflections |
141|-----+---------+--------------+------------+--------------+------------+-----------------|
142| 0 | 0 | 1 | 183 | 0 | 91.5 | 27247 |
143| 1 | 0 | 181 | 363 | 90 | 181.5 | 23642 |
144| 2 | 0 | 361 | 543 | 180 | 271.5 | 24634 |
145| 3 | 0 | 541 | 720 | 270 | 360 | 23236 |
146+-----+---------+--------------+------------+--------------+------------+-----------------+
147
148 Using multiprocessing with 4 parallel job(s)
149
150
151 Frames: 1 -> 183
152
153 Number of reflections
154 Partial: 93
155 Full: 27154
156 In ice ring: 0
157 Total: 27247
158
159
160 Frames: 181 -> 363
161
162 Number of reflections
163 Partial: 7
164 Full: 23635
165 In ice ring: 0
166 Total: 23642
167
168
169 Frames: 361 -> 543
170
171 Number of reflections
172 Partial: 10
173 Full: 24624
174 In ice ring: 0
175 Total: 24634
176
177
178 Frames: 541 -> 720
179
180 Number of reflections
181 Partial: 78
182 Full: 23158
183 In ice ring: 0
184 Total: 23236
185
186
187 Summary of profile model
188+------+-----------+-----------+----------+----------+----------+-----------------+
189| ID | Profile | Created | X (px) | Y (px) | Z (im) | # reflections |
190|------+-----------+-----------+----------+----------+----------+-----------------|
191| 0 | 0 | True | 410.5 | 421.17 | 5 | 1690 |
192| 0 | 1 | True | 1231.5 | 421.17 | 5 | 2008 |
193| 0 | 2 | True | 2052.5 | 421.17 | 5 | 1805 |
194| 0 | 3 | True | 410.5 | 1263.5 | 5 | 2348 |
195| 0 | 4 | True | 1231.5 | 1263.5 | 5 | 2824 |
196| 0 | 5 | True | 2052.5 | 1263.5 | 5 | 2574 |
197| 0 | 6 | True | 410.5 | 2105.83 | 5 | 1764 |
198| 0 | 7 | True | 1231.5 | 2105.83 | 5 | 2179 |
199| 0 | 8 | True | 2052.5 | 2105.83 | 5 | 1972 |
200| 0 | 9 | True | 410.5 | 421.17 | 15 | 2562 |
201| 0 | 10 | True | 1231.5 | 421.17 | 15 | 3053 |
202| 0 | 11 | True | 2052.5 | 421.17 | 15 | 2730 |
203| 0 | 12 | True | 410.5 | 1263.5 | 15 | 3557 |
204| 0 | 13 | True | 1231.5 | 1263.5 | 15 | 4280 |
205| 0 | 14 | True | 2052.5 | 1263.5 | 15 | 3877 |
206| 0 | 15 | True | 410.5 | 2105.83 | 15 | 2667 |
207| 0 | 16 | True | 1231.5 | 2105.83 | 15 | 3291 |
208| 0 | 17 | True | 2052.5 | 2105.83 | 15 | 2964 |
209| 0 | 18 | True | 410.5 | 421.17 | 25 | 2642 |
210| 0 | 19 | True | 1231.5 | 421.17 | 25 | 3148 |
211| 0 | 20 | True | 2052.5 | 421.17 | 25 | 2790 |
212| 0 | 21 | True | 410.5 | 1263.5 | 25 | 3616 |
213| 0 | 22 | True | 1231.5 | 1263.5 | 25 | 4328 |
214| 0 | 23 | True | 2052.5 | 1263.5 | 25 | 3893 |
215| 0 | 24 | True | 410.5 | 2105.83 | 25 | 2627 |
216| 0 | 25 | True | 1231.5 | 2105.83 | 25 | 3220 |
217| 0 | 26 | True | 2052.5 | 2105.83 | 25 | 2886 |
218| 0 | 27 | True | 410.5 | 421.17 | 35 | 2703 |
219| 0 | 28 | True | 1231.5 | 421.17 | 35 | 3219 |
220| 0 | 29 | True | 2052.5 | 421.17 | 35 | 2850 |
221| 0 | 30 | True | 410.5 | 1263.5 | 35 | 3662 |
222| 0 | 31 | True | 1231.5 | 1263.5 | 35 | 4360 |
223| 0 | 32 | True | 2052.5 | 1263.5 | 35 | 3913 |
224| 0 | 33 | True | 410.5 | 2105.83 | 35 | 2579 |
225| 0 | 34 | True | 1231.5 | 2105.83 | 35 | 3147 |
226| 0 | 35 | True | 2052.5 | 2105.83 | 35 | 2820 |
227| 0 | 36 | True | 410.5 | 421.17 | 45 | 2764 |
228| 0 | 37 | True | 1231.5 | 421.17 | 45 | 3278 |
229| 0 | 38 | True | 2052.5 | 421.17 | 45 | 2904 |
230| 0 | 39 | True | 410.5 | 1263.5 | 45 | 3647 |
231| 0 | 40 | True | 1231.5 | 1263.5 | 45 | 4309 |
232| 0 | 41 | True | 2052.5 | 1263.5 | 45 | 3882 |
233| 0 | 42 | True | 410.5 | 2105.83 | 45 | 2461 |
234| 0 | 43 | True | 1231.5 | 2105.83 | 45 | 2983 |
235| 0 | 44 | True | 2052.5 | 2105.83 | 45 | 2697 |
236| 0 | 45 | True | 410.5 | 421.17 | 55 | 2831 |
237| 0 | 46 | True | 1231.5 | 421.17 | 55 | 3342 |
238| 0 | 47 | True | 2052.5 | 421.17 | 55 | 2958 |
239| 0 | 48 | True | 410.5 | 1263.5 | 55 | 3645 |
240| 0 | 49 | True | 1231.5 | 1263.5 | 55 | 4282 |
241| 0 | 50 | True | 2052.5 | 1263.5 | 55 | 3850 |
242| 0 | 51 | True | 410.5 | 2105.83 | 55 | 2392 |
243| 0 | 52 | True | 1231.5 | 2105.83 | 55 | 2880 |
244| 0 | 53 | True | 2052.5 | 2105.83 | 55 | 2605 |
245| 0 | 54 | True | 410.5 | 421.17 | 65 | 2883 |
246| 0 | 55 | True | 1231.5 | 421.17 | 65 | 3413 |
247| 0 | 56 | True | 2052.5 | 421.17 | 65 | 2996 |
248| 0 | 57 | True | 410.5 | 1263.5 | 65 | 3639 |
249| 0 | 58 | True | 1231.5 | 1263.5 | 65 | 4276 |
250| 0 | 59 | True | 2052.5 | 1263.5 | 65 | 3822 |
251| 0 | 60 | True | 410.5 | 2105.83 | 65 | 2309 |
252| 0 | 61 | True | 1231.5 | 2105.83 | 65 | 2770 |
253| 0 | 62 | True | 2052.5 | 2105.83 | 65 | 2504 |
254| 0 | 63 | True | 410.5 | 421.17 | 75 | 2989 |
255| 0 | 64 | True | 1231.5 | 421.17 | 75 | 3544 |
256| 0 | 65 | True | 2052.5 | 421.17 | 75 | 3083 |
257| 0 | 66 | True | 410.5 | 1263.5 | 75 | 3680 |
258| 0 | 67 | True | 1231.5 | 1263.5 | 75 | 4336 |
259| 0 | 68 | True | 2052.5 | 1263.5 | 75 | 3840 |
260| 0 | 69 | True | 410.5 | 2105.83 | 75 | 2248 |
261| 0 | 70 | True | 1231.5 | 2105.83 | 75 | 2709 |
262| 0 | 71 | True | 2052.5 | 2105.83 | 75 | 2434 |
263| 0 | 72 | True | 410.5 | 421.17 | 85 | 3030 |
264| 0 | 73 | True | 1231.5 | 421.17 | 85 | 3620 |
265| 0 | 74 | True | 2052.5 | 421.17 | 85 | 3140 |
266| 0 | 75 | True | 410.5 | 1263.5 | 85 | 3686 |
267| 0 | 76 | True | 1231.5 | 1263.5 | 85 | 4375 |
268| 0 | 77 | True | 2052.5 | 1263.5 | 85 | 3869 |
269| 0 | 78 | True | 410.5 | 2105.83 | 85 | 2177 |
270| 0 | 79 | True | 1231.5 | 2105.83 | 85 | 2655 |
271| 0 | 80 | True | 2052.5 | 2105.83 | 85 | 2410 |
272| 0 | 81 | True | 410.5 | 421.17 | 95 | 3145 |
273| 0 | 82 | True | 1231.5 | 421.17 | 95 | 3751 |
274| 0 | 83 | True | 2052.5 | 421.17 | 95 | 3232 |
275| 0 | 84 | True | 410.5 | 1263.5 | 95 | 3751 |
276| 0 | 85 | True | 1231.5 | 1263.5 | 95 | 4452 |
277| 0 | 86 | True | 2052.5 | 1263.5 | 95 | 3914 |
278| 0 | 87 | True | 410.5 | 2105.83 | 95 | 2168 |
279| 0 | 88 | True | 1231.5 | 2105.83 | 95 | 2652 |
280| 0 | 89 | True | 2052.5 | 2105.83 | 95 | 2405 |
281| 0 | 90 | True | 410.5 | 421.17 | 105 | 3181 |
282| 0 | 91 | True | 1231.5 | 421.17 | 105 | 3792 |
283| 0 | 92 | True | 2052.5 | 421.17 | 105 | 3284 |
284| 0 | 93 | True | 410.5 | 1263.5 | 105 | 3763 |
285| 0 | 94 | True | 1231.5 | 1263.5 | 105 | 4464 |
286| 0 | 95 | True | 2052.5 | 1263.5 | 105 | 3936 |
287| 0 | 96 | True | 410.5 | 2105.83 | 105 | 2143 |
288| 0 | 97 | True | 1231.5 | 2105.83 | 105 | 2617 |
289| 0 | 98 | True | 2052.5 | 2105.83 | 105 | 2389 |
290| 0 | 99 | True | 410.5 | 421.17 | 115 | 3283 |
291| 0 | 100 | True | 1231.5 | 421.17 | 115 | 3896 |
292| 0 | 101 | True | 2052.5 | 421.17 | 115 | 3352 |
293| 0 | 102 | True | 410.5 | 1263.5 | 115 | 3814 |
294| 0 | 103 | True | 1231.5 | 1263.5 | 115 | 4503 |
295| 0 | 104 | True | 2052.5 | 1263.5 | 115 | 3936 |
296| 0 | 105 | True | 410.5 | 2105.83 | 115 | 2159 |
297| 0 | 106 | True | 1231.5 | 2105.83 | 115 | 2616 |
298| 0 | 107 | True | 2052.5 | 2105.83 | 115 | 2361 |
299| 0 | 108 | True | 410.5 | 421.17 | 125 | 3239 |
300| 0 | 109 | True | 1231.5 | 421.17 | 125 | 3831 |
301| 0 | 110 | True | 2052.5 | 421.17 | 125 | 3265 |
302| 0 | 111 | True | 410.5 | 1263.5 | 125 | 3722 |
303| 0 | 112 | True | 1231.5 | 1263.5 | 125 | 4385 |
304| 0 | 113 | True | 2052.5 | 1263.5 | 125 | 3794 |
305| 0 | 114 | True | 410.5 | 2105.83 | 125 | 2140 |
306| 0 | 115 | True | 1231.5 | 2105.83 | 125 | 2582 |
307| 0 | 116 | True | 2052.5 | 2105.83 | 125 | 2313 |
308| 0 | 117 | True | 410.5 | 421.17 | 135 | 3210 |
309| 0 | 118 | True | 1231.5 | 421.17 | 135 | 3777 |
310| 0 | 119 | True | 2052.5 | 421.17 | 135 | 3193 |
311| 0 | 120 | True | 410.5 | 1263.5 | 135 | 3660 |
312| 0 | 121 | True | 1231.5 | 1263.5 | 135 | 4292 |
313| 0 | 122 | True | 2052.5 | 1263.5 | 135 | 3682 |
314| 0 | 123 | True | 410.5 | 2105.83 | 135 | 2146 |
315| 0 | 124 | True | 1231.5 | 2105.83 | 135 | 2577 |
316| 0 | 125 | True | 2052.5 | 2105.83 | 135 | 2284 |
317| 0 | 126 | True | 410.5 | 421.17 | 145 | 3110 |
318| 0 | 127 | True | 1231.5 | 421.17 | 145 | 3658 |
319| 0 | 128 | True | 2052.5 | 421.17 | 145 | 3101 |
320| 0 | 129 | True | 410.5 | 1263.5 | 145 | 3552 |
321| 0 | 130 | True | 1231.5 | 1263.5 | 145 | 4164 |
322| 0 | 131 | True | 2052.5 | 1263.5 | 145 | 3582 |
323| 0 | 132 | True | 410.5 | 2105.83 | 145 | 2150 |
324| 0 | 133 | True | 1231.5 | 2105.83 | 145 | 2576 |
325| 0 | 134 | True | 2052.5 | 2105.83 | 145 | 2287 |
326| 0 | 135 | True | 410.5 | 421.17 | 155 | 3047 |
327| 0 | 136 | True | 1231.5 | 421.17 | 155 | 3582 |
328| 0 | 137 | True | 2052.5 | 421.17 | 155 | 3061 |
329| 0 | 138 | True | 410.5 | 1263.5 | 155 | 3493 |
330| 0 | 139 | True | 1231.5 | 1263.5 | 155 | 4091 |
331| 0 | 140 | True | 2052.5 | 1263.5 | 155 | 3549 |
332| 0 | 141 | True | 410.5 | 2105.83 | 155 | 2151 |
333| 0 | 142 | True | 1231.5 | 2105.83 | 155 | 2587 |
334| 0 | 143 | True | 2052.5 | 2105.83 | 155 | 2303 |
335| 0 | 144 | True | 410.5 | 421.17 | 165 | 3024 |
336| 0 | 145 | True | 1231.5 | 421.17 | 165 | 3550 |
337| 0 | 146 | True | 2052.5 | 421.17 | 165 | 3021 |
338| 0 | 147 | True | 410.5 | 1263.5 | 165 | 3478 |
339| 0 | 148 | True | 1231.5 | 1263.5 | 165 | 4064 |
340| 0 | 149 | True | 2052.5 | 1263.5 | 165 | 3516 |
341| 0 | 150 | True | 410.5 | 2105.83 | 165 | 2192 |
342| 0 | 151 | True | 1231.5 | 2105.83 | 165 | 2633 |
343| 0 | 152 | True | 2052.5 | 2105.83 | 165 | 2332 |
344| 0 | 153 | True | 410.5 | 421.17 | 175 | 2950 |
345| 0 | 154 | True | 1231.5 | 421.17 | 175 | 3467 |
346| 0 | 155 | True | 2052.5 | 421.17 | 175 | 2938 |
347| 0 | 156 | True | 410.5 | 1263.5 | 175 | 3395 |
348| 0 | 157 | True | 1231.5 | 1263.5 | 175 | 3965 |
349| 0 | 158 | True | 2052.5 | 1263.5 | 175 | 3424 |
350| 0 | 159 | True | 410.5 | 2105.83 | 175 | 2191 |
351| 0 | 160 | True | 1231.5 | 2105.83 | 175 | 2631 |
352| 0 | 161 | True | 2052.5 | 2105.83 | 175 | 2322 |
353| 0 | 162 | True | 410.5 | 421.17 | 185 | 2907 |
354| 0 | 163 | True | 1231.5 | 421.17 | 185 | 3412 |
355| 0 | 164 | True | 2052.5 | 421.17 | 185 | 2894 |
356| 0 | 165 | True | 410.5 | 1263.5 | 185 | 3334 |
357| 0 | 166 | True | 1231.5 | 1263.5 | 185 | 3888 |
358| 0 | 167 | True | 2052.5 | 1263.5 | 185 | 3359 |
359| 0 | 168 | True | 410.5 | 2105.83 | 185 | 2221 |
360| 0 | 169 | True | 1231.5 | 2105.83 | 185 | 2655 |
361| 0 | 170 | True | 2052.5 | 2105.83 | 185 | 2337 |
362| 0 | 171 | True | 410.5 | 421.17 | 195 | 2798 |
363| 0 | 172 | True | 1231.5 | 421.17 | 195 | 3298 |
364| 0 | 173 | True | 2052.5 | 421.17 | 195 | 2813 |
365| 0 | 174 | True | 410.5 | 1263.5 | 195 | 3223 |
366| 0 | 175 | True | 1231.5 | 1263.5 | 195 | 3770 |
367| 0 | 176 | True | 2052.5 | 1263.5 | 195 | 3270 |
368| 0 | 177 | True | 410.5 | 2105.83 | 195 | 2244 |
369| 0 | 178 | True | 1231.5 | 2105.83 | 195 | 2678 |
370| 0 | 179 | True | 2052.5 | 2105.83 | 195 | 2356 |
371| 0 | 180 | True | 410.5 | 421.17 | 205 | 2714 |
372| 0 | 181 | True | 1231.5 | 421.17 | 205 | 3195 |
373| 0 | 182 | True | 2052.5 | 421.17 | 205 | 2723 |
374| 0 | 183 | True | 410.5 | 1263.5 | 205 | 3116 |
375| 0 | 184 | True | 1231.5 | 1263.5 | 205 | 3658 |
376| 0 | 185 | True | 2052.5 | 1263.5 | 205 | 3166 |
377| 0 | 186 | True | 410.5 | 2105.83 | 205 | 2227 |
378| 0 | 187 | True | 1231.5 | 2105.83 | 205 | 2677 |
379| 0 | 188 | True | 2052.5 | 2105.83 | 205 | 2337 |
380| 0 | 189 | True | 410.5 | 421.17 | 215 | 2636 |
381| 0 | 190 | True | 1231.5 | 421.17 | 215 | 3097 |
382| 0 | 191 | True | 2052.5 | 421.17 | 215 | 2633 |
383| 0 | 192 | True | 410.5 | 1263.5 | 215 | 3060 |
384| 0 | 193 | True | 1231.5 | 1263.5 | 215 | 3594 |
385| 0 | 194 | True | 2052.5 | 1263.5 | 215 | 3108 |
386| 0 | 195 | True | 410.5 | 2105.83 | 215 | 2240 |
387| 0 | 196 | True | 1231.5 | 2105.83 | 215 | 2682 |
388| 0 | 197 | True | 2052.5 | 2105.83 | 215 | 2335 |
389| 0 | 198 | True | 410.5 | 421.17 | 225 | 2536 |
390| 0 | 199 | True | 1231.5 | 421.17 | 225 | 2989 |
391| 0 | 200 | True | 2052.5 | 421.17 | 225 | 2529 |
392| 0 | 201 | True | 410.5 | 1263.5 | 225 | 2972 |
393| 0 | 202 | True | 1231.5 | 1263.5 | 225 | 3502 |
394| 0 | 203 | True | 2052.5 | 1263.5 | 225 | 3018 |
395| 0 | 204 | True | 410.5 | 2105.83 | 225 | 2204 |
396| 0 | 205 | True | 1231.5 | 2105.83 | 225 | 2644 |
397| 0 | 206 | True | 2052.5 | 2105.83 | 225 | 2299 |
398| 0 | 207 | True | 410.5 | 421.17 | 235 | 2567 |
399| 0 | 208 | True | 1231.5 | 421.17 | 235 | 3005 |
400| 0 | 209 | True | 2052.5 | 421.17 | 235 | 2543 |
401| 0 | 210 | True | 410.5 | 1263.5 | 235 | 3046 |
402| 0 | 211 | True | 1231.5 | 1263.5 | 235 | 3569 |
403| 0 | 212 | True | 2052.5 | 1263.5 | 235 | 3081 |
404| 0 | 213 | True | 410.5 | 2105.83 | 235 | 2280 |
405| 0 | 214 | True | 1231.5 | 2105.83 | 235 | 2713 |
406| 0 | 215 | True | 2052.5 | 2105.83 | 235 | 2364 |
407| 0 | 216 | True | 410.5 | 421.17 | 245 | 2550 |
408| 0 | 217 | True | 1231.5 | 421.17 | 245 | 2988 |
409| 0 | 218 | True | 2052.5 | 421.17 | 245 | 2523 |
410| 0 | 219 | True | 410.5 | 1263.5 | 245 | 3057 |
411| 0 | 220 | True | 1231.5 | 1263.5 | 245 | 3579 |
412| 0 | 221 | True | 2052.5 | 1263.5 | 245 | 3076 |
413| 0 | 222 | True | 410.5 | 2105.83 | 245 | 2306 |
414| 0 | 223 | True | 1231.5 | 2105.83 | 245 | 2742 |
415| 0 | 224 | True | 2052.5 | 2105.83 | 245 | 2377 |
416| 0 | 225 | True | 410.5 | 421.17 | 255 | 2621 |
417| 0 | 226 | True | 1231.5 | 421.17 | 255 | 3056 |
418| 0 | 227 | True | 2052.5 | 421.17 | 255 | 2589 |
419| 0 | 228 | True | 410.5 | 1263.5 | 255 | 3157 |
420| 0 | 229 | True | 1231.5 | 1263.5 | 255 | 3691 |
421| 0 | 230 | True | 2052.5 | 1263.5 | 255 | 3179 |
422| 0 | 231 | True | 410.5 | 2105.83 | 255 | 2375 |
423| 0 | 232 | True | 1231.5 | 2105.83 | 255 | 2834 |
424| 0 | 233 | True | 2052.5 | 2105.83 | 255 | 2451 |
425| 0 | 234 | True | 410.5 | 421.17 | 265 | 2617 |
426| 0 | 235 | True | 1231.5 | 421.17 | 265 | 3036 |
427| 0 | 236 | True | 2052.5 | 421.17 | 265 | 2560 |
428| 0 | 237 | True | 410.5 | 1263.5 | 265 | 3211 |
429| 0 | 238 | True | 1231.5 | 1263.5 | 265 | 3729 |
430| 0 | 239 | True | 2052.5 | 1263.5 | 265 | 3185 |
431| 0 | 240 | True | 410.5 | 2105.83 | 265 | 2444 |
432| 0 | 241 | True | 1231.5 | 2105.83 | 265 | 2895 |
433| 0 | 242 | True | 2052.5 | 2105.83 | 265 | 2463 |
434| 0 | 243 | True | 410.5 | 421.17 | 275 | 2619 |
435| 0 | 244 | True | 1231.5 | 421.17 | 275 | 3019 |
436| 0 | 245 | True | 2052.5 | 421.17 | 275 | 2548 |
437| 0 | 246 | True | 410.5 | 1263.5 | 275 | 3272 |
438| 0 | 247 | True | 1231.5 | 1263.5 | 275 | 3772 |
439| 0 | 248 | True | 2052.5 | 1263.5 | 275 | 3217 |
440| 0 | 249 | True | 410.5 | 2105.83 | 275 | 2498 |
441| 0 | 250 | True | 1231.5 | 2105.83 | 275 | 2946 |
442| 0 | 251 | True | 2052.5 | 2105.83 | 275 | 2483 |
443| 0 | 252 | True | 410.5 | 421.17 | 285 | 2562 |
444| 0 | 253 | True | 1231.5 | 421.17 | 285 | 2942 |
445| 0 | 254 | True | 2052.5 | 421.17 | 285 | 2484 |
446| 0 | 255 | True | 410.5 | 1263.5 | 285 | 3292 |
447| 0 | 256 | True | 1231.5 | 1263.5 | 285 | 3768 |
448| 0 | 257 | True | 2052.5 | 1263.5 | 285 | 3203 |
449| 0 | 258 | True | 410.5 | 2105.83 | 285 | 2558 |
450| 0 | 259 | True | 1231.5 | 2105.83 | 285 | 2986 |
451| 0 | 260 | True | 2052.5 | 2105.83 | 285 | 2497 |
452| 0 | 261 | True | 410.5 | 421.17 | 295 | 2505 |
453| 0 | 262 | True | 1231.5 | 421.17 | 295 | 2905 |
454| 0 | 263 | True | 2052.5 | 421.17 | 295 | 2471 |
455| 0 | 264 | True | 410.5 | 1263.5 | 295 | 3286 |
456| 0 | 265 | True | 1231.5 | 1263.5 | 295 | 3792 |
457| 0 | 266 | True | 2052.5 | 1263.5 | 295 | 3239 |
458| 0 | 267 | True | 410.5 | 2105.83 | 295 | 2571 |
459| 0 | 268 | True | 1231.5 | 2105.83 | 295 | 3024 |
460| 0 | 269 | True | 2052.5 | 2105.83 | 295 | 2541 |
461| 0 | 270 | True | 410.5 | 421.17 | 305 | 2473 |
462| 0 | 271 | True | 1231.5 | 421.17 | 305 | 2883 |
463| 0 | 272 | True | 2052.5 | 421.17 | 305 | 2466 |
464| 0 | 273 | True | 410.5 | 1263.5 | 305 | 3309 |
465| 0 | 274 | True | 1231.5 | 1263.5 | 305 | 3835 |
466| 0 | 275 | True | 2052.5 | 1263.5 | 305 | 3280 |
467| 0 | 276 | True | 410.5 | 2105.83 | 305 | 2627 |
468| 0 | 277 | True | 1231.5 | 2105.83 | 305 | 3098 |
469| 0 | 278 | True | 2052.5 | 2105.83 | 305 | 2612 |
470| 0 | 279 | True | 410.5 | 421.17 | 315 | 2459 |
471| 0 | 280 | True | 1231.5 | 421.17 | 315 | 2881 |
472| 0 | 281 | True | 2052.5 | 421.17 | 315 | 2466 |
473| 0 | 282 | True | 410.5 | 1263.5 | 315 | 3338 |
474| 0 | 283 | True | 1231.5 | 1263.5 | 315 | 3880 |
475| 0 | 284 | True | 2052.5 | 1263.5 | 315 | 3308 |
476| 0 | 285 | True | 410.5 | 2105.83 | 315 | 2669 |
477| 0 | 286 | True | 1231.5 | 2105.83 | 315 | 3145 |
478| 0 | 287 | True | 2052.5 | 2105.83 | 315 | 2637 |
479| 0 | 288 | True | 410.5 | 421.17 | 325 | 2412 |
480| 0 | 289 | True | 1231.5 | 421.17 | 325 | 2831 |
481| 0 | 290 | True | 2052.5 | 421.17 | 325 | 2443 |
482| 0 | 291 | True | 410.5 | 1263.5 | 325 | 3336 |
483| 0 | 292 | True | 1231.5 | 1263.5 | 325 | 3875 |
484| 0 | 293 | True | 2052.5 | 1263.5 | 325 | 3314 |
485| 0 | 294 | True | 410.5 | 2105.83 | 325 | 2686 |
486| 0 | 295 | True | 1231.5 | 2105.83 | 325 | 3155 |
487| 0 | 296 | True | 2052.5 | 2105.83 | 325 | 2649 |
488| 0 | 297 | True | 410.5 | 421.17 | 335 | 2360 |
489| 0 | 298 | True | 1231.5 | 421.17 | 335 | 2793 |
490| 0 | 299 | True | 2052.5 | 421.17 | 335 | 2423 |
491| 0 | 300 | True | 410.5 | 1263.5 | 335 | 3323 |
492| 0 | 301 | True | 1231.5 | 1263.5 | 335 | 3876 |
493| 0 | 302 | True | 2052.5 | 1263.5 | 335 | 3318 |
494| 0 | 303 | True | 410.5 | 2105.83 | 335 | 2682 |
495| 0 | 304 | True | 1231.5 | 2105.83 | 335 | 3154 |
496| 0 | 305 | True | 2052.5 | 2105.83 | 335 | 2640 |
497| 0 | 306 | True | 410.5 | 421.17 | 345 | 2359 |
498| 0 | 307 | True | 1231.5 | 421.17 | 345 | 2816 |
499| 0 | 308 | True | 2052.5 | 421.17 | 345 | 2463 |
500| 0 | 309 | True | 410.5 | 1263.5 | 345 | 3351 |
501| 0 | 310 | True | 1231.5 | 1263.5 | 345 | 3930 |
502| 0 | 311 | True | 2052.5 | 1263.5 | 345 | 3411 |
503| 0 | 312 | True | 410.5 | 2105.83 | 345 | 2698 |
504| 0 | 313 | True | 1231.5 | 2105.83 | 345 | 3188 |
505| 0 | 314 | True | 2052.5 | 2105.83 | 345 | 2710 |
506| 0 | 315 | True | 410.5 | 421.17 | 355 | 2404 |
507| 0 | 316 | True | 1231.5 | 421.17 | 355 | 2878 |
508| 0 | 317 | True | 2052.5 | 421.17 | 355 | 2545 |
509| 0 | 318 | True | 410.5 | 1263.5 | 355 | 3430 |
510| 0 | 319 | True | 1231.5 | 1263.5 | 355 | 4021 |
511| 0 | 320 | True | 2052.5 | 1263.5 | 355 | 3532 |
512| 0 | 321 | True | 410.5 | 2105.83 | 355 | 2722 |
513| 0 | 322 | True | 1231.5 | 2105.83 | 355 | 3217 |
514| 0 | 323 | True | 2052.5 | 2105.83 | 355 | 2765 |
515| 0 | 324 | True | 410.5 | 421.17 | 365 | 2436 |
516| 0 | 325 | True | 1231.5 | 421.17 | 365 | 2933 |
517| 0 | 326 | True | 2052.5 | 421.17 | 365 | 2617 |
518| 0 | 327 | True | 410.5 | 1263.5 | 365 | 3442 |
519| 0 | 328 | True | 1231.5 | 1263.5 | 365 | 4052 |
520| 0 | 329 | True | 2052.5 | 1263.5 | 365 | 3601 |
521| 0 | 330 | True | 410.5 | 2105.83 | 365 | 2682 |
522| 0 | 331 | True | 1231.5 | 2105.83 | 365 | 3181 |
523| 0 | 332 | True | 2052.5 | 2105.83 | 365 | 2765 |
524| 0 | 333 | True | 410.5 | 421.17 | 375 | 2461 |
525| 0 | 334 | True | 1231.5 | 421.17 | 375 | 2960 |
526| 0 | 335 | True | 2052.5 | 421.17 | 375 | 2657 |
527| 0 | 336 | True | 410.5 | 1263.5 | 375 | 3466 |
528| 0 | 337 | True | 1231.5 | 1263.5 | 375 | 4070 |
529| 0 | 338 | True | 2052.5 | 1263.5 | 375 | 3620 |
530| 0 | 339 | True | 410.5 | 2105.83 | 375 | 2652 |
531| 0 | 340 | True | 1231.5 | 2105.83 | 375 | 3133 |
532| 0 | 341 | True | 2052.5 | 2105.83 | 375 | 2724 |
533| 0 | 342 | True | 410.5 | 421.17 | 385 | 2473 |
534| 0 | 343 | True | 1231.5 | 421.17 | 385 | 2988 |
535| 0 | 344 | True | 2052.5 | 421.17 | 385 | 2686 |
536| 0 | 345 | True | 410.5 | 1263.5 | 385 | 3436 |
537| 0 | 346 | True | 1231.5 | 1263.5 | 385 | 4047 |
538| 0 | 347 | True | 2052.5 | 1263.5 | 385 | 3607 |
539| 0 | 348 | True | 410.5 | 2105.83 | 385 | 2560 |
540| 0 | 349 | True | 1231.5 | 2105.83 | 385 | 3034 |
541| 0 | 350 | True | 2052.5 | 2105.83 | 385 | 2645 |
542| 0 | 351 | True | 410.5 | 421.17 | 395 | 2517 |
543| 0 | 352 | True | 1231.5 | 421.17 | 395 | 3050 |
544| 0 | 353 | True | 2052.5 | 421.17 | 395 | 2740 |
545| 0 | 354 | True | 410.5 | 1263.5 | 395 | 3473 |
546| 0 | 355 | True | 1231.5 | 1263.5 | 395 | 4096 |
547| 0 | 356 | True | 2052.5 | 1263.5 | 395 | 3652 |
548| 0 | 357 | True | 410.5 | 2105.83 | 395 | 2526 |
549| 0 | 358 | True | 1231.5 | 2105.83 | 395 | 2996 |
550| 0 | 359 | True | 2052.5 | 2105.83 | 395 | 2617 |
551| 0 | 360 | True | 410.5 | 421.17 | 405 | 2548 |
552| 0 | 361 | True | 1231.5 | 421.17 | 405 | 3098 |
553| 0 | 362 | True | 2052.5 | 421.17 | 405 | 2796 |
554| 0 | 363 | True | 410.5 | 1263.5 | 405 | 3440 |
555| 0 | 364 | True | 1231.5 | 1263.5 | 405 | 4072 |
556| 0 | 365 | True | 2052.5 | 1263.5 | 405 | 3661 |
557| 0 | 366 | True | 410.5 | 2105.83 | 405 | 2414 |
558| 0 | 367 | True | 1231.5 | 2105.83 | 405 | 2876 |
559| 0 | 368 | True | 2052.5 | 2105.83 | 405 | 2532 |
560| 0 | 369 | True | 410.5 | 421.17 | 415 | 2592 |
561| 0 | 370 | True | 1231.5 | 421.17 | 415 | 3175 |
562| 0 | 371 | True | 2052.5 | 421.17 | 415 | 2879 |
563| 0 | 372 | True | 410.5 | 1263.5 | 415 | 3428 |
564| 0 | 373 | True | 1231.5 | 1263.5 | 415 | 4090 |
565| 0 | 374 | True | 2052.5 | 1263.5 | 415 | 3703 |
566| 0 | 375 | True | 410.5 | 2105.83 | 415 | 2351 |
567| 0 | 376 | True | 1231.5 | 2105.83 | 415 | 2806 |
568| 0 | 377 | True | 2052.5 | 2105.83 | 415 | 2501 |
569| 0 | 378 | True | 410.5 | 421.17 | 425 | 2635 |
570| 0 | 379 | True | 1231.5 | 421.17 | 425 | 3238 |
571| 0 | 380 | True | 2052.5 | 421.17 | 425 | 2945 |
572| 0 | 381 | True | 410.5 | 1263.5 | 425 | 3400 |
573| 0 | 382 | True | 1231.5 | 1263.5 | 425 | 4074 |
574| 0 | 383 | True | 2052.5 | 1263.5 | 425 | 3710 |
575| 0 | 384 | True | 410.5 | 2105.83 | 425 | 2266 |
576| 0 | 385 | True | 1231.5 | 2105.83 | 425 | 2700 |
577| 0 | 386 | True | 2052.5 | 2105.83 | 425 | 2434 |
578| 0 | 387 | True | 410.5 | 421.17 | 435 | 2668 |
579| 0 | 388 | True | 1231.5 | 421.17 | 435 | 3302 |
580| 0 | 389 | True | 2052.5 | 421.17 | 435 | 3006 |
581| 0 | 390 | True | 410.5 | 1263.5 | 435 | 3360 |
582| 0 | 391 | True | 1231.5 | 1263.5 | 435 | 4054 |
583| 0 | 392 | True | 2052.5 | 1263.5 | 435 | 3693 |
584| 0 | 393 | True | 410.5 | 2105.83 | 435 | 2188 |
585| 0 | 394 | True | 1231.5 | 2105.83 | 435 | 2601 |
586| 0 | 395 | True | 2052.5 | 2105.83 | 435 | 2347 |
587| 0 | 396 | True | 410.5 | 421.17 | 445 | 2703 |
588| 0 | 397 | True | 1231.5 | 421.17 | 445 | 3350 |
589| 0 | 398 | True | 2052.5 | 421.17 | 445 | 3032 |
590| 0 | 399 | True | 410.5 | 1263.5 | 445 | 3319 |
591| 0 | 400 | True | 1231.5 | 1263.5 | 445 | 4010 |
592| 0 | 401 | True | 2052.5 | 1263.5 | 445 | 3637 |
593| 0 | 402 | True | 410.5 | 2105.83 | 445 | 2109 |
594| 0 | 403 | True | 1231.5 | 2105.83 | 445 | 2499 |
595| 0 | 404 | True | 2052.5 | 2105.83 | 445 | 2243 |
596| 0 | 405 | True | 410.5 | 421.17 | 455 | 2799 |
597| 0 | 406 | True | 1231.5 | 421.17 | 455 | 3476 |
598| 0 | 407 | True | 2052.5 | 421.17 | 455 | 3148 |
599| 0 | 408 | True | 410.5 | 1263.5 | 455 | 3359 |
600| 0 | 409 | True | 1231.5 | 1263.5 | 455 | 4073 |
601| 0 | 410 | True | 2052.5 | 1263.5 | 455 | 3700 |
602| 0 | 411 | True | 410.5 | 2105.83 | 455 | 2086 |
603| 0 | 412 | True | 1231.5 | 2105.83 | 455 | 2467 |
604| 0 | 413 | True | 2052.5 | 2105.83 | 455 | 2220 |
605| 0 | 414 | True | 410.5 | 421.17 | 465 | 2872 |
606| 0 | 415 | True | 1231.5 | 421.17 | 465 | 3550 |
607| 0 | 416 | True | 2052.5 | 421.17 | 465 | 3203 |
608| 0 | 417 | True | 410.5 | 1263.5 | 465 | 3393 |
609| 0 | 418 | True | 1231.5 | 1263.5 | 465 | 4105 |
610| 0 | 419 | True | 2052.5 | 1263.5 | 465 | 3716 |
611| 0 | 420 | True | 410.5 | 2105.83 | 465 | 2055 |
612| 0 | 421 | True | 1231.5 | 2105.83 | 465 | 2436 |
613| 0 | 422 | True | 2052.5 | 2105.83 | 465 | 2191 |
614| 0 | 423 | True | 410.5 | 421.17 | 475 | 2887 |
615| 0 | 424 | True | 1231.5 | 421.17 | 475 | 3580 |
616| 0 | 425 | True | 2052.5 | 421.17 | 475 | 3232 |
617| 0 | 426 | True | 410.5 | 1263.5 | 475 | 3345 |
618| 0 | 427 | True | 1231.5 | 1263.5 | 475 | 4068 |
619| 0 | 428 | True | 2052.5 | 1263.5 | 475 | 3683 |
620| 0 | 429 | True | 410.5 | 2105.83 | 475 | 2003 |
621| 0 | 430 | True | 1231.5 | 2105.83 | 475 | 2386 |
622| 0 | 431 | True | 2052.5 | 2105.83 | 475 | 2151 |
623| 0 | 432 | True | 410.5 | 421.17 | 485 | 2825 |
624| 0 | 433 | True | 1231.5 | 421.17 | 485 | 3510 |
625| 0 | 434 | True | 2052.5 | 421.17 | 485 | 3163 |
626| 0 | 435 | True | 410.5 | 1263.5 | 485 | 3218 |
627| 0 | 436 | True | 1231.5 | 1263.5 | 485 | 3922 |
628| 0 | 437 | True | 2052.5 | 1263.5 | 485 | 3540 |
629| 0 | 438 | True | 410.5 | 2105.83 | 485 | 1941 |
630| 0 | 439 | True | 1231.5 | 2105.83 | 485 | 2312 |
631| 0 | 440 | True | 2052.5 | 2105.83 | 485 | 2079 |
632| 0 | 441 | True | 410.5 | 421.17 | 495 | 2756 |
633| 0 | 442 | True | 1231.5 | 421.17 | 495 | 3448 |
634| 0 | 443 | True | 2052.5 | 421.17 | 495 | 3107 |
635| 0 | 444 | True | 410.5 | 1263.5 | 495 | 3102 |
636| 0 | 445 | True | 1231.5 | 1263.5 | 495 | 3815 |
637| 0 | 446 | True | 2052.5 | 1263.5 | 495 | 3446 |
638| 0 | 447 | True | 410.5 | 2105.83 | 495 | 1898 |
639| 0 | 448 | True | 1231.5 | 2105.83 | 495 | 2276 |
640| 0 | 449 | True | 2052.5 | 2105.83 | 495 | 2048 |
641| 0 | 450 | True | 410.5 | 421.17 | 505 | 2763 |
642| 0 | 451 | True | 1231.5 | 421.17 | 505 | 3434 |
643| 0 | 452 | True | 2052.5 | 421.17 | 505 | 3099 |
644| 0 | 453 | True | 410.5 | 1263.5 | 505 | 3095 |
645| 0 | 454 | True | 1231.5 | 1263.5 | 505 | 3787 |
646| 0 | 455 | True | 2052.5 | 1263.5 | 505 | 3428 |
647| 0 | 456 | True | 410.5 | 2105.83 | 505 | 1932 |
648| 0 | 457 | True | 1231.5 | 2105.83 | 505 | 2308 |
649| 0 | 458 | True | 2052.5 | 2105.83 | 505 | 2070 |
650| 0 | 459 | True | 410.5 | 421.17 | 515 | 2701 |
651| 0 | 460 | True | 1231.5 | 421.17 | 515 | 3347 |
652| 0 | 461 | True | 2052.5 | 421.17 | 515 | 3024 |
653| 0 | 462 | True | 410.5 | 1263.5 | 515 | 3024 |
654| 0 | 463 | True | 1231.5 | 1263.5 | 515 | 3697 |
655| 0 | 464 | True | 2052.5 | 1263.5 | 515 | 3350 |
656| 0 | 465 | True | 410.5 | 2105.83 | 515 | 1921 |
657| 0 | 466 | True | 1231.5 | 2105.83 | 515 | 2309 |
658| 0 | 467 | True | 2052.5 | 2105.83 | 515 | 2060 |
659| 0 | 468 | True | 410.5 | 421.17 | 525 | 2686 |
660| 0 | 469 | True | 1231.5 | 421.17 | 525 | 3326 |
661| 0 | 470 | True | 2052.5 | 421.17 | 525 | 3015 |
662| 0 | 471 | True | 410.5 | 1263.5 | 525 | 2980 |
663| 0 | 472 | True | 1231.5 | 1263.5 | 525 | 3644 |
664| 0 | 473 | True | 2052.5 | 1263.5 | 525 | 3312 |
665| 0 | 474 | True | 410.5 | 2105.83 | 525 | 1908 |
666| 0 | 475 | True | 1231.5 | 2105.83 | 525 | 2300 |
667| 0 | 476 | True | 2052.5 | 2105.83 | 525 | 2050 |
668| 0 | 477 | True | 410.5 | 421.17 | 535 | 2603 |
669| 0 | 478 | True | 1231.5 | 421.17 | 535 | 3261 |
670| 0 | 479 | True | 2052.5 | 421.17 | 535 | 2958 |
671| 0 | 480 | True | 410.5 | 1263.5 | 535 | 2899 |
672| 0 | 481 | True | 1231.5 | 1263.5 | 535 | 3578 |
673| 0 | 482 | True | 2052.5 | 1263.5 | 535 | 3251 |
674| 0 | 483 | True | 410.5 | 2105.83 | 535 | 1904 |
675| 0 | 484 | True | 1231.5 | 2105.83 | 535 | 2312 |
676| 0 | 485 | True | 2052.5 | 2105.83 | 535 | 2059 |
677| 0 | 486 | True | 410.5 | 421.17 | 545 | 2594 |
678| 0 | 487 | True | 1231.5 | 421.17 | 545 | 3270 |
679| 0 | 488 | True | 2052.5 | 421.17 | 545 | 2975 |
680| 0 | 489 | True | 410.5 | 1263.5 | 545 | 2867 |
681| 0 | 490 | True | 1231.5 | 1263.5 | 545 | 3563 |
682| 0 | 491 | True | 2052.5 | 1263.5 | 545 | 3247 |
683| 0 | 492 | True | 410.5 | 2105.83 | 545 | 1900 |
684| 0 | 493 | True | 1231.5 | 2105.83 | 545 | 2321 |
685| 0 | 494 | True | 2052.5 | 2105.83 | 545 | 2079 |
686| 0 | 495 | True | 410.5 | 421.17 | 555 | 2532 |
687| 0 | 496 | True | 1231.5 | 421.17 | 555 | 3195 |
688| 0 | 497 | True | 2052.5 | 421.17 | 555 | 2908 |
689| 0 | 498 | True | 410.5 | 1263.5 | 555 | 2822 |
690| 0 | 499 | True | 1231.5 | 1263.5 | 555 | 3510 |
691| 0 | 500 | True | 2052.5 | 1263.5 | 555 | 3196 |
692| 0 | 501 | True | 410.5 | 2105.83 | 555 | 1944 |
693| 0 | 502 | True | 1231.5 | 2105.83 | 555 | 2382 |
694| 0 | 503 | True | 2052.5 | 2105.83 | 555 | 2135 |
695| 0 | 504 | True | 410.5 | 421.17 | 565 | 2465 |
696| 0 | 505 | True | 1231.5 | 421.17 | 565 | 3106 |
697| 0 | 506 | True | 2052.5 | 421.17 | 565 | 2821 |
698| 0 | 507 | True | 410.5 | 1263.5 | 565 | 2750 |
699| 0 | 508 | True | 1231.5 | 1263.5 | 565 | 3425 |
700| 0 | 509 | True | 2052.5 | 1263.5 | 565 | 3105 |
701| 0 | 510 | True | 410.5 | 2105.83 | 565 | 1927 |
702| 0 | 511 | True | 1231.5 | 2105.83 | 565 | 2380 |
703| 0 | 512 | True | 2052.5 | 2105.83 | 565 | 2118 |
704| 0 | 513 | True | 410.5 | 421.17 | 575 | 2439 |
705| 0 | 514 | True | 1231.5 | 421.17 | 575 | 3076 |
706| 0 | 515 | True | 2052.5 | 421.17 | 575 | 2795 |
707| 0 | 516 | True | 410.5 | 1263.5 | 575 | 2786 |
708| 0 | 517 | True | 1231.5 | 1263.5 | 575 | 3470 |
709| 0 | 518 | True | 2052.5 | 1263.5 | 575 | 3143 |
710| 0 | 519 | True | 410.5 | 2105.83 | 575 | 1990 |
711| 0 | 520 | True | 1231.5 | 2105.83 | 575 | 2482 |
712| 0 | 521 | True | 2052.5 | 2105.83 | 575 | 2212 |
713| 0 | 522 | True | 410.5 | 421.17 | 585 | 2402 |
714| 0 | 523 | True | 1231.5 | 421.17 | 585 | 3042 |
715| 0 | 524 | True | 2052.5 | 421.17 | 585 | 2763 |
716| 0 | 525 | True | 410.5 | 1263.5 | 585 | 2801 |
717| 0 | 526 | True | 1231.5 | 1263.5 | 585 | 3496 |
718| 0 | 527 | True | 2052.5 | 1263.5 | 585 | 3175 |
719| 0 | 528 | True | 410.5 | 2105.83 | 585 | 2024 |
720| 0 | 529 | True | 1231.5 | 2105.83 | 585 | 2537 |
721| 0 | 530 | True | 2052.5 | 2105.83 | 585 | 2271 |
722| 0 | 531 | True | 410.5 | 421.17 | 595 | 2439 |
723| 0 | 532 | True | 1231.5 | 421.17 | 595 | 3081 |
724| 0 | 533 | True | 2052.5 | 421.17 | 595 | 2817 |
725| 0 | 534 | True | 410.5 | 1263.5 | 595 | 2908 |
726| 0 | 535 | True | 1231.5 | 1263.5 | 595 | 3623 |
727| 0 | 536 | True | 2052.5 | 1263.5 | 595 | 3316 |
728| 0 | 537 | True | 410.5 | 2105.83 | 595 | 2124 |
729| 0 | 538 | True | 1231.5 | 2105.83 | 595 | 2664 |
730| 0 | 539 | True | 2052.5 | 2105.83 | 595 | 2410 |
731| 0 | 540 | True | 410.5 | 421.17 | 605 | 2431 |
732| 0 | 541 | True | 1231.5 | 421.17 | 605 | 3066 |
733| 0 | 542 | True | 2052.5 | 421.17 | 605 | 2796 |
734| 0 | 543 | True | 410.5 | 1263.5 | 605 | 2944 |
735| 0 | 544 | True | 1231.5 | 1263.5 | 605 | 3664 |
736| 0 | 545 | True | 2052.5 | 1263.5 | 605 | 3349 |
737| 0 | 546 | True | 410.5 | 2105.83 | 605 | 2186 |
738| 0 | 547 | True | 1231.5 | 2105.83 | 605 | 2730 |
739| 0 | 548 | True | 2052.5 | 2105.83 | 605 | 2460 |
740| 0 | 549 | True | 410.5 | 421.17 | 615 | 2481 |
741| 0 | 550 | True | 1231.5 | 421.17 | 615 | 3097 |
742| 0 | 551 | True | 2052.5 | 421.17 | 615 | 2799 |
743| 0 | 552 | True | 410.5 | 1263.5 | 615 | 3015 |
744| 0 | 553 | True | 1231.5 | 1263.5 | 615 | 3731 |
745| 0 | 554 | True | 2052.5 | 1263.5 | 615 | 3381 |
746| 0 | 555 | True | 410.5 | 2105.83 | 615 | 2261 |
747| 0 | 556 | True | 1231.5 | 2105.83 | 615 | 2811 |
748| 0 | 557 | True | 2052.5 | 2105.83 | 615 | 2515 |
749| 0 | 558 | True | 410.5 | 421.17 | 625 | 2427 |
750| 0 | 559 | True | 1231.5 | 421.17 | 625 | 3011 |
751| 0 | 560 | True | 2052.5 | 421.17 | 625 | 2699 |
752| 0 | 561 | True | 410.5 | 1263.5 | 625 | 2963 |
753| 0 | 562 | True | 1231.5 | 1263.5 | 625 | 3655 |
754| 0 | 563 | True | 2052.5 | 1263.5 | 625 | 3298 |
755| 0 | 564 | True | 410.5 | 2105.83 | 625 | 2266 |
756| 0 | 565 | True | 1231.5 | 2105.83 | 625 | 2820 |
757| 0 | 566 | True | 2052.5 | 2105.83 | 625 | 2519 |
758| 0 | 567 | True | 410.5 | 421.17 | 635 | 2349 |
759| 0 | 568 | True | 1231.5 | 421.17 | 635 | 2884 |
760| 0 | 569 | True | 2052.5 | 421.17 | 635 | 2578 |
761| 0 | 570 | True | 410.5 | 1263.5 | 635 | 2878 |
762| 0 | 571 | True | 1231.5 | 1263.5 | 635 | 3530 |
763| 0 | 572 | True | 2052.5 | 1263.5 | 635 | 3184 |
764| 0 | 573 | True | 410.5 | 2105.83 | 635 | 2247 |
765| 0 | 574 | True | 1231.5 | 2105.83 | 635 | 2795 |
766| 0 | 575 | True | 2052.5 | 2105.83 | 635 | 2497 |
767| 0 | 576 | True | 410.5 | 421.17 | 645 | 2282 |
768| 0 | 577 | True | 1231.5 | 421.17 | 645 | 2800 |
769| 0 | 578 | True | 2052.5 | 421.17 | 645 | 2502 |
770| 0 | 579 | True | 410.5 | 1263.5 | 645 | 2886 |
771| 0 | 580 | True | 1231.5 | 1263.5 | 645 | 3542 |
772| 0 | 581 | True | 2052.5 | 1263.5 | 645 | 3196 |
773| 0 | 582 | True | 410.5 | 2105.83 | 645 | 2319 |
774| 0 | 583 | True | 1231.5 | 2105.83 | 645 | 2886 |
775| 0 | 584 | True | 2052.5 | 2105.83 | 645 | 2576 |
776| 0 | 585 | True | 410.5 | 421.17 | 655 | 2302 |
777| 0 | 586 | True | 1231.5 | 421.17 | 655 | 2825 |
778| 0 | 587 | True | 2052.5 | 421.17 | 655 | 2505 |
779| 0 | 588 | True | 410.5 | 1263.5 | 655 | 2982 |
780| 0 | 589 | True | 1231.5 | 1263.5 | 655 | 3677 |
781| 0 | 590 | True | 2052.5 | 1263.5 | 655 | 3297 |
782| 0 | 591 | True | 410.5 | 2105.83 | 655 | 2414 |
783| 0 | 592 | True | 1231.5 | 2105.83 | 655 | 3020 |
784| 0 | 593 | True | 2052.5 | 2105.83 | 655 | 2674 |
785| 0 | 594 | True | 410.5 | 421.17 | 665 | 2346 |
786| 0 | 595 | True | 1231.5 | 421.17 | 665 | 2876 |
787| 0 | 596 | True | 2052.5 | 421.17 | 665 | 2544 |
788| 0 | 597 | True | 410.5 | 1263.5 | 665 | 3110 |
789| 0 | 598 | True | 1231.5 | 1263.5 | 665 | 3835 |
790| 0 | 599 | True | 2052.5 | 1263.5 | 665 | 3430 |
791| 0 | 600 | True | 410.5 | 2105.83 | 665 | 2553 |
792| 0 | 601 | True | 1231.5 | 2105.83 | 665 | 3180 |
793| 0 | 602 | True | 2052.5 | 2105.83 | 665 | 2809 |
794| 0 | 603 | True | 410.5 | 421.17 | 675 | 2347 |
795| 0 | 604 | True | 1231.5 | 421.17 | 675 | 2883 |
796| 0 | 605 | True | 2052.5 | 421.17 | 675 | 2556 |
797| 0 | 606 | True | 410.5 | 1263.5 | 675 | 3128 |
798| 0 | 607 | True | 1231.5 | 1263.5 | 675 | 3872 |
799| 0 | 608 | True | 2052.5 | 1263.5 | 675 | 3466 |
800| 0 | 609 | True | 410.5 | 2105.83 | 675 | 2573 |
801| 0 | 610 | True | 1231.5 | 2105.83 | 675 | 3218 |
802| 0 | 611 | True | 2052.5 | 2105.83 | 675 | 2847 |
803| 0 | 612 | True | 410.5 | 421.17 | 685 | 2337 |
804| 0 | 613 | True | 1231.5 | 421.17 | 685 | 2841 |
805| 0 | 614 | True | 2052.5 | 421.17 | 685 | 2525 |
806| 0 | 615 | True | 410.5 | 1263.5 | 685 | 3165 |
807| 0 | 616 | True | 1231.5 | 1263.5 | 685 | 3885 |
808| 0 | 617 | True | 2052.5 | 1263.5 | 685 | 3480 |
809| 0 | 618 | True | 410.5 | 2105.83 | 685 | 2618 |
810| 0 | 619 | True | 1231.5 | 2105.83 | 685 | 3247 |
811| 0 | 620 | True | 2052.5 | 2105.83 | 685 | 2882 |
812| 0 | 621 | True | 410.5 | 421.17 | 695 | 2336 |
813| 0 | 622 | True | 1231.5 | 421.17 | 695 | 2836 |
814| 0 | 623 | True | 2052.5 | 421.17 | 695 | 2504 |
815| 0 | 624 | True | 410.5 | 1263.5 | 695 | 3203 |
816| 0 | 625 | True | 1231.5 | 1263.5 | 695 | 3959 |
817| 0 | 626 | True | 2052.5 | 1263.5 | 695 | 3538 |
818| 0 | 627 | True | 410.5 | 2105.83 | 695 | 2628 |
819| 0 | 628 | True | 1231.5 | 2105.83 | 695 | 3296 |
820| 0 | 629 | True | 2052.5 | 2105.83 | 695 | 2925 |
821| 0 | 630 | True | 410.5 | 421.17 | 705 | 2342 |
822| 0 | 631 | True | 1231.5 | 421.17 | 705 | 2812 |
823| 0 | 632 | True | 2052.5 | 421.17 | 705 | 2480 |
824| 0 | 633 | True | 410.5 | 1263.5 | 705 | 3306 |
825| 0 | 634 | True | 1231.5 | 1263.5 | 705 | 4072 |
826| 0 | 635 | True | 2052.5 | 1263.5 | 705 | 3646 |
827| 0 | 636 | True | 410.5 | 2105.83 | 705 | 2700 |
828| 0 | 637 | True | 1231.5 | 2105.83 | 705 | 3387 |
829| 0 | 638 | True | 2052.5 | 2105.83 | 705 | 3015 |
830| 0 | 639 | True | 410.5 | 421.17 | 715 | 1564 |
831| 0 | 640 | True | 1231.5 | 421.17 | 715 | 1881 |
832| 0 | 641 | True | 2052.5 | 421.17 | 715 | 1659 |
833| 0 | 642 | True | 410.5 | 1263.5 | 715 | 2232 |
834| 0 | 643 | True | 1231.5 | 1263.5 | 715 | 2765 |
835| 0 | 644 | True | 2052.5 | 1263.5 | 715 | 2480 |
836| 0 | 645 | True | 410.5 | 2105.83 | 715 | 1818 |
837| 0 | 646 | True | 1231.5 | 2105.83 | 715 | 2294 |
838| 0 | 647 | True | 2052.5 | 2105.83 | 715 | 2045 |
839+------+-----------+-----------+----------+----------+----------+-----------------+
840
841
842Timing information for reference profile formation
843+-------------------+---------------+
844| Read time | 50.17 seconds |
845| Extract time | 0.55 seconds |
846| Pre-process time | 0.12 seconds |
847| Process time | 28.79 seconds |
848| Post-process time | 0.00 seconds |
849| Total time | 79.90 seconds |
850+-------------------+---------------+
851
852================================================================================
853
854Integrating reflections
855
856 Split 111 reflections overlapping job boundaries
857
858Memory situation report:
859 Available system memory : 201.2 GB
860 Maximum memory for processing : 181.1 GB
861 Memory required per process : 0.0 GB
862
863Processing reflections in the following blocks of images:
864
865 block_size: Auto
866
867+-----+---------+--------------+------------+--------------+------------+-----------------+
868| # | Group | Frame From | Frame To | Angle From | Angle To | # Reflections |
869|-----+---------+--------------+------------+--------------+------------+-----------------|
870| 0 | 0 | 1 | 183 | 0 | 91.5 | 93302 |
871| 1 | 0 | 181 | 363 | 90 | 181.5 | 91596 |
872| 2 | 0 | 361 | 543 | 180 | 271.5 | 91206 |
873| 3 | 0 | 541 | 720 | 270 | 360 | 92160 |
874+-----+---------+--------------+------------+--------------+------------+-----------------+
875
876 Using multiprocessing with 4 parallel job(s)
877
878
879 Frames: 0 -> 183
880
881 Number of reflections
882 Partial: 1210
883 Full: 92092
884 In ice ring: 0
885 Integrate: 93302
886 Total: 93302
887
888
889 Frames: 180 -> 363
890
891 Number of reflections
892 Partial: 40
893 Full: 91556
894 In ice ring: 0
895 Integrate: 91596
896 Total: 91596
897
898
899 Frames: 360 -> 543
900
901 Number of reflections
902 Partial: 50
903 Full: 91156
904 In ice ring: 0
905 Integrate: 91206
906 Total: 91206
907
908
909 Frames: 540 -> 720
910
911 Number of reflections
912 Partial: 1273
913 Full: 90887
914 In ice ring: 0
915 Integrate: 92160
916 Total: 92160
917
918
919 Summary vs image number
920+------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------+
921| ID | Image | # full | # part | # over | # ice | # sum | # prf | Ibg | I/sigI | I/sigI | CC prf | RMSD XY |
922| | | | | | | | | | (sum) | (prf) | | |
923|------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------|
924| 0 | 1 | 297 | 1178 | 0 | 0 | 1269 | 480 | 0.75 | 3.86 | 9.55 | 0.74 | 0.64 |
925| 0 | 2 | 473 | 14 | 0 | 0 | 417 | 429 | 0.72 | 7.01 | 6.97 | 0.72 | 0.43 |
926| 0 | 3 | 495 | 4 | 0 | 0 | 429 | 446 | 0.7 | 6.47 | 6.39 | 0.71 | 0.43 |
927| 0 | 4 | 507 | 1 | 0 | 0 | 425 | 443 | 0.7 | 7.35 | 7.12 | 0.72 | 0.42 |
928| 0 | 5 | 530 | 1 | 0 | 0 | 454 | 472 | 0.76 | 8.42 | 8.4 | 0.72 | 0.43 |
929| 0 | 6 | 507 | 1 | 0 | 0 | 441 | 453 | 0.65 | 6.63 | 6.5 | 0.72 | 0.45 |
930| 0 | 7 | 535 | 1 | 0 | 0 | 457 | 481 | 0.77 | 8.77 | 8.64 | 0.72 | 0.43 |
931| 0 | 8 | 550 | 0 | 0 | 0 | 460 | 480 | 0.73 | 7.71 | 7.68 | 0.72 | 0.43 |
932| 0 | 9 | 500 | 1 | 0 | 0 | 423 | 439 | 0.65 | 7.71 | 7.52 | 0.71 | 0.41 |
933| 0 | 10 | 481 | 0 | 0 | 0 | 409 | 428 | 0.68 | 8.7 | 8.36 | 0.72 | 0.43 |
934| 0 | 11 | 469 | 1 | 0 | 0 | 399 | 414 | 0.72 | 7.41 | 7.27 | 0.72 | 0.43 |
935| 0 | 12 | 518 | 0 | 0 | 0 | 445 | 457 | 0.73 | 7.85 | 7.73 | 0.73 | 0.43 |
936| 0 | 13 | 512 | 0 | 0 | 0 | 430 | 441 | 0.74 | 7.34 | 7.2 | 0.73 | 0.44 |
937| 0 | 14 | 503 | 0 | 0 | 0 | 435 | 455 | 0.75 | 8.99 | 8.8 | 0.72 | 0.42 |
938| 0 | 15 | 499 | 0 | 0 | 0 | 426 | 453 | 0.67 | 6.89 | 6.6 | 0.71 | 0.46 |
939| 0 | 16 | 520 | 0 | 0 | 0 | 445 | 465 | 0.69 | 6.91 | 6.84 | 0.72 | 0.46 |
940| 0 | 17 | 524 | 0 | 0 | 0 | 445 | 467 | 0.64 | 6.54 | 6.39 | 0.71 | 0.43 |
941| 0 | 18 | 513 | 0 | 0 | 0 | 436 | 453 | 0.74 | 6.92 | 6.84 | 0.72 | 0.41 |
942| 0 | 19 | 491 | 0 | 0 | 0 | 403 | 420 | 0.7 | 6.71 | 6.48 | 0.71 | 0.43 |
943| 0 | 20 | 531 | 0 | 0 | 0 | 455 | 473 | 0.7 | 7.7 | 7.5 | 0.71 | 0.43 |
944| 0 | 21 | 512 | 0 | 0 | 0 | 433 | 447 | 0.73 | 8.29 | 8.25 | 0.72 | 0.43 |
945| 0 | 22 | 515 | 0 | 0 | 0 | 439 | 463 | 0.74 | 7.49 | 7.32 | 0.72 | 0.43 |
946| 0 | 23 | 485 | 0 | 0 | 0 | 422 | 436 | 0.63 | 7.05 | 6.88 | 0.71 | 0.44 |
947| 0 | 24 | 498 | 0 | 0 | 0 | 414 | 434 | 0.68 | 7.53 | 7.31 | 0.72 | 0.44 |
948| 0 | 25 | 511 | 0 | 0 | 0 | 439 | 461 | 0.62 | 6.56 | 6.49 | 0.7 | 0.44 |
949| 0 | 26 | 536 | 0 | 0 | 0 | 469 | 482 | 0.68 | 7.75 | 7.67 | 0.72 | 0.44 |
950| 0 | 27 | 498 | 0 | 0 | 0 | 434 | 445 | 0.74 | 8.12 | 8.03 | 0.73 | 0.45 |
951| 0 | 28 | 504 | 0 | 0 | 0 | 432 | 449 | 0.68 | 7.48 | 7.31 | 0.71 | 0.43 |
952| 0 | 29 | 526 | 0 | 0 | 0 | 456 | 470 | 0.76 | 9.13 | 9.06 | 0.71 | 0.44 |
953| 0 | 30 | 494 | 0 | 0 | 0 | 425 | 439 | 0.72 | 7.35 | 7.21 | 0.71 | 0.45 |
954| 0 | 31 | 522 | 0 | 0 | 0 | 440 | 456 | 0.68 | 7.48 | 7.27 | 0.72 | 0.44 |
955| 0 | 32 | 541 | 0 | 0 | 0 | 446 | 476 | 0.74 | 7.96 | 7.69 | 0.72 | 0.43 |
956| 0 | 33 | 480 | 0 | 0 | 0 | 411 | 428 | 0.66 | 6.92 | 6.81 | 0.72 | 0.42 |
957| 0 | 34 | 517 | 0 | 0 | 0 | 448 | 468 | 0.66 | 6.69 | 6.6 | 0.72 | 0.43 |
958| 0 | 35 | 513 | 0 | 0 | 0 | 444 | 461 | 0.64 | 6.1 | 6 | 0.71 | 0.46 |
959| 0 | 36 | 479 | 0 | 0 | 0 | 410 | 427 | 0.65 | 7.21 | 7.45 | 0.72 | 0.45 |
960| 0 | 37 | 504 | 0 | 0 | 0 | 427 | 439 | 0.67 | 6.29 | 6.18 | 0.71 | 0.47 |
961| 0 | 38 | 517 | 0 | 0 | 0 | 425 | 452 | 0.66 | 6.59 | 6.47 | 0.72 | 0.45 |
962| 0 | 39 | 489 | 0 | 0 | 0 | 406 | 427 | 0.65 | 7.09 | 6.92 | 0.72 | 0.45 |
963| 0 | 40 | 532 | 0 | 0 | 0 | 464 | 485 | 0.74 | 7.83 | 7.64 | 0.72 | 0.45 |
964| 0 | 41 | 491 | 0 | 0 | 0 | 425 | 440 | 0.74 | 8.35 | 8.23 | 0.73 | 0.44 |
965| 0 | 42 | 524 | 0 | 0 | 0 | 437 | 463 | 0.73 | 7.08 | 6.95 | 0.72 | 0.41 |
966| 0 | 43 | 495 | 0 | 0 | 0 | 432 | 446 | 0.66 | 7.28 | 7.15 | 0.72 | 0.44 |
967| 0 | 44 | 499 | 0 | 0 | 0 | 415 | 438 | 0.68 | 7.43 | 7.24 | 0.72 | 0.44 |
968| 0 | 45 | 534 | 0 | 0 | 0 | 450 | 463 | 0.65 | 6.93 | 6.74 | 0.71 | 0.47 |
969| 0 | 46 | 475 | 0 | 0 | 0 | 413 | 426 | 0.68 | 7.84 | 7.79 | 0.71 | 0.45 |
970| 0 | 47 | 528 | 0 | 0 | 0 | 453 | 474 | 0.7 | 7.26 | 7.1 | 0.71 | 0.46 |
971| 0 | 48 | 489 | 0 | 0 | 0 | 422 | 437 | 0.71 | 7.74 | 7.61 | 0.72 | 0.42 |
972| 0 | 49 | 520 | 0 | 0 | 0 | 446 | 465 | 0.64 | 6.9 | 6.88 | 0.7 | 0.47 |
973| 0 | 50 | 510 | 0 | 0 | 0 | 440 | 455 | 0.71 | 7.78 | 7.62 | 0.73 | 0.41 |
974| 0 | 51 | 524 | 0 | 0 | 0 | 437 | 457 | 0.63 | 6.61 | 6.39 | 0.7 | 0.47 |
975| 0 | 52 | 494 | 0 | 0 | 0 | 423 | 441 | 0.68 | 7.83 | 7.75 | 0.73 | 0.41 |
976| 0 | 53 | 530 | 0 | 0 | 0 | 455 | 476 | 0.67 | 7.5 | 7.28 | 0.71 | 0.46 |
977| 0 | 54 | 494 | 0 | 0 | 0 | 416 | 435 | 0.7 | 7.78 | 7.77 | 0.74 | 0.41 |
978| 0 | 55 | 533 | 0 | 0 | 0 | 454 | 483 | 0.62 | 6.74 | 6.53 | 0.7 | 0.46 |
979| 0 | 56 | 488 | 0 | 0 | 0 | 411 | 424 | 0.71 | 6.89 | 7.03 | 0.72 | 0.44 |
980| 0 | 57 | 526 | 0 | 0 | 0 | 441 | 465 | 0.64 | 6.23 | 6.05 | 0.7 | 0.46 |
981| 0 | 58 | 491 | 0 | 0 | 0 | 434 | 444 | 0.7 | 7.68 | 7.6 | 0.73 | 0.42 |
982| 0 | 59 | 522 | 0 | 0 | 0 | 446 | 471 | 0.62 | 6.81 | 6.68 | 0.71 | 0.44 |
983| 0 | 60 | 487 | 0 | 0 | 0 | 398 | 420 | 0.71 | 7.95 | 7.7 | 0.72 | 0.42 |
984| 0 | 61 | 533 | 0 | 0 | 0 | 460 | 476 | 0.67 | 6.75 | 6.59 | 0.72 | 0.43 |
985| 0 | 62 | 470 | 0 | 0 | 0 | 404 | 420 | 0.64 | 6.49 | 6.47 | 0.72 | 0.45 |
986| 0 | 63 | 530 | 0 | 0 | 0 | 452 | 470 | 0.72 | 7.24 | 7.08 | 0.72 | 0.43 |
987| 0 | 64 | 503 | 0 | 0 | 0 | 418 | 436 | 0.68 | 7.79 | 7.57 | 0.72 | 0.46 |
988| 0 | 65 | 506 | 0 | 0 | 0 | 434 | 452 | 0.66 | 6.86 | 6.81 | 0.71 | 0.45 |
989| 0 | 66 | 524 | 0 | 0 | 0 | 446 | 465 | 0.69 | 7.61 | 7.52 | 0.73 | 0.46 |
990| 0 | 67 | 490 | 0 | 0 | 0 | 424 | 440 | 0.69 | 7.5 | 7.41 | 0.71 | 0.47 |
991| 0 | 68 | 519 | 0 | 0 | 0 | 441 | 459 | 0.68 | 7.87 | 7.65 | 0.73 | 0.42 |
992| 0 | 69 | 525 | 0 | 0 | 0 | 441 | 462 | 0.66 | 6.65 | 6.49 | 0.71 | 0.46 |
993| 0 | 70 | 472 | 0 | 0 | 0 | 406 | 420 | 0.67 | 7.16 | 6.95 | 0.73 | 0.44 |
994| 0 | 71 | 527 | 0 | 0 | 0 | 450 | 464 | 0.72 | 8.43 | 8.33 | 0.73 | 0.42 |
995| 0 | 72 | 501 | 0 | 0 | 0 | 438 | 451 | 0.6 | 6.56 | 6.38 | 0.71 | 0.45 |
996| 0 | 73 | 533 | 0 | 0 | 0 | 452 | 473 | 0.7 | 7.02 | 6.88 | 0.73 | 0.43 |
997| 0 | 74 | 523 | 0 | 0 | 0 | 441 | 461 | 0.66 | 6.48 | 6.56 | 0.71 | 0.43 |
998| 0 | 75 | 476 | 0 | 0 | 0 | 416 | 433 | 0.64 | 6.28 | 6.16 | 0.71 | 0.43 |
999| 0 | 76 | 556 | 0 | 0 | 0 | 470 | 484 | 0.64 | 6.95 | 6.85 | 0.72 | 0.44 |
1000| 0 | 77 | 484 | 0 | 0 | 0 | 406 | 424 | 0.69 | 7.17 | 7.22 | 0.73 | 0.44 |
1001| 0 | 78 | 507 | 0 | 0 | 0 | 424 | 445 | 0.65 | 6.77 | 6.54 | 0.71 | 0.45 |
1002| 0 | 79 | 512 | 0 | 0 | 0 | 435 | 454 | 0.68 | 7.15 | 7.14 | 0.72 | 0.43 |
1003| 0 | 80 | 508 | 0 | 0 | 0 | 430 | 449 | 0.67 | 7.46 | 7.28 | 0.72 | 0.43 |
1004| 0 | 81 | 521 | 0 | 0 | 0 | 429 | 459 | 0.71 | 7.86 | 7.52 | 0.71 | 0.44 |
1005| 0 | 82 | 485 | 0 | 0 | 0 | 410 | 429 | 0.7 | 6.89 | 6.87 | 0.72 | 0.42 |
1006| 0 | 83 | 531 | 0 | 0 | 0 | 451 | 469 | 0.71 | 6.76 | 6.7 | 0.72 | 0.45 |
1007| 0 | 84 | 493 | 0 | 0 | 0 | 427 | 443 | 0.66 | 7.07 | 6.91 | 0.72 | 0.43 |
1008| 0 | 85 | 495 | 0 | 0 | 0 | 413 | 439 | 0.63 | 6.54 | 6.72 | 0.73 | 0.4 |
1009| 0 | 86 | 499 | 0 | 0 | 0 | 421 | 443 | 0.65 | 6.96 | 6.86 | 0.72 | 0.45 |
1010| 0 | 87 | 477 | 0 | 0 | 0 | 388 | 400 | 0.62 | 6.43 | 6.39 | 0.72 | 0.43 |
1011| 0 | 88 | 551 | 0 | 0 | 0 | 484 | 507 | 0.73 | 8.15 | 8.01 | 0.73 | 0.43 |
1012| 0 | 89 | 510 | 0 | 0 | 0 | 428 | 446 | 0.68 | 6.75 | 6.65 | 0.73 | 0.41 |
1013| 0 | 90 | 514 | 0 | 0 | 0 | 433 | 448 | 0.71 | 7.78 | 7.6 | 0.72 | 0.41 |
1014| 0 | 91 | 529 | 0 | 0 | 0 | 455 | 472 | 0.65 | 6.42 | 6.46 | 0.72 | 0.44 |
1015| 0 | 92 | 504 | 0 | 0 | 0 | 434 | 453 | 0.7 | 7.55 | 7.37 | 0.73 | 0.42 |
1016| 0 | 93 | 526 | 0 | 0 | 0 | 459 | 476 | 0.61 | 6.2 | 6.17 | 0.72 | 0.45 |
1017| 0 | 94 | 491 | 0 | 0 | 0 | 420 | 437 | 0.61 | 5.76 | 5.6 | 0.72 | 0.42 |
1018| 0 | 95 | 515 | 0 | 0 | 0 | 436 | 459 | 0.66 | 6.72 | 6.52 | 0.72 | 0.43 |
1019| 0 | 96 | 526 | 0 | 0 | 0 | 435 | 463 | 0.71 | 8.12 | 7.89 | 0.72 | 0.41 |
1020| 0 | 97 | 476 | 0 | 0 | 0 | 414 | 431 | 0.69 | 6.9 | 7.05 | 0.73 | 0.42 |
1021| 0 | 98 | 540 | 0 | 0 | 0 | 471 | 486 | 0.72 | 7.18 | 7.11 | 0.73 | 0.45 |
1022| 0 | 99 | 468 | 0 | 0 | 0 | 387 | 407 | 0.71 | 7.18 | 7.07 | 0.72 | 0.44 |
1023| 0 | 100 | 460 | 0 | 0 | 0 | 389 | 407 | 0.65 | 7.06 | 7.14 | 0.72 | 0.41 |
1024| 0 | 101 | 505 | 0 | 0 | 0 | 435 | 457 | 0.65 | 6.83 | 6.69 | 0.72 | 0.41 |
1025| 0 | 102 | 544 | 0 | 0 | 0 | 459 | 477 | 0.69 | 6.25 | 6.47 | 0.72 | 0.42 |
1026| 0 | 103 | 539 | 0 | 0 | 0 | 464 | 475 | 0.69 | 7.94 | 7.91 | 0.72 | 0.43 |
1027| 0 | 104 | 522 | 0 | 0 | 0 | 453 | 473 | 0.66 | 6.79 | 6.68 | 0.72 | 0.41 |
1028| 0 | 105 | 508 | 0 | 0 | 0 | 435 | 456 | 0.69 | 6.52 | 6.51 | 0.73 | 0.43 |
1029| 0 | 106 | 508 | 0 | 0 | 0 | 444 | 460 | 0.65 | 7.64 | 7.48 | 0.72 | 0.43 |
1030| 0 | 107 | 511 | 0 | 0 | 0 | 428 | 451 | 0.63 | 6.71 | 6.5 | 0.71 | 0.46 |
1031| 0 | 108 | 479 | 0 | 0 | 0 | 402 | 415 | 0.71 | 7.96 | 7.84 | 0.73 | 0.4 |
1032| 0 | 109 | 545 | 0 | 0 | 0 | 464 | 488 | 0.74 | 7.08 | 7.13 | 0.74 | 0.41 |
1033| 0 | 110 | 495 | 0 | 0 | 0 | 424 | 441 | 0.73 | 7.68 | 7.78 | 0.73 | 0.4 |
1034| 0 | 111 | 464 | 0 | 0 | 0 | 393 | 411 | 0.7 | 6.79 | 6.9 | 0.72 | 0.45 |
1035| 0 | 112 | 503 | 0 | 0 | 0 | 421 | 439 | 0.65 | 6.47 | 6.32 | 0.71 | 0.44 |
1036| 0 | 113 | 554 | 0 | 0 | 0 | 469 | 491 | 0.7 | 7.48 | 7.47 | 0.73 | 0.4 |
1037| 0 | 114 | 502 | 0 | 0 | 0 | 439 | 454 | 0.66 | 6.62 | 6.5 | 0.72 | 0.41 |
1038| 0 | 115 | 528 | 0 | 0 | 0 | 443 | 460 | 0.69 | 7.24 | 7.21 | 0.72 | 0.42 |
1039| 0 | 116 | 515 | 0 | 0 | 0 | 419 | 441 | 0.67 | 6.57 | 6.57 | 0.72 | 0.43 |
1040| 0 | 117 | 501 | 0 | 0 | 0 | 417 | 442 | 0.69 | 7.14 | 6.81 | 0.73 | 0.4 |
1041| 0 | 118 | 501 | 0 | 0 | 0 | 439 | 452 | 0.72 | 7.66 | 7.62 | 0.73 | 0.41 |
1042| 0 | 119 | 518 | 0 | 0 | 0 | 442 | 459 | 0.76 | 7.69 | 7.47 | 0.73 | 0.41 |
1043| 0 | 120 | 477 | 0 | 0 | 0 | 409 | 432 | 0.68 | 6.54 | 6.39 | 0.72 | 0.41 |
1044| 0 | 121 | 487 | 0 | 0 | 0 | 413 | 433 | 0.69 | 6.47 | 6.5 | 0.72 | 0.45 |
1045| 0 | 122 | 557 | 0 | 0 | 0 | 472 | 489 | 0.73 | 6.74 | 6.67 | 0.73 | 0.42 |
1046| 0 | 123 | 496 | 0 | 0 | 0 | 428 | 440 | 0.66 | 6.28 | 6.2 | 0.72 | 0.42 |
1047| 0 | 124 | 533 | 0 | 0 | 0 | 452 | 472 | 0.68 | 6.69 | 6.57 | 0.71 | 0.42 |
1048| 0 | 125 | 510 | 0 | 0 | 0 | 444 | 456 | 0.74 | 7.1 | 7.04 | 0.73 | 0.45 |
1049| 0 | 126 | 508 | 0 | 0 | 0 | 433 | 456 | 0.76 | 7.77 | 7.78 | 0.75 | 0.41 |
1050| 0 | 127 | 519 | 0 | 0 | 0 | 446 | 463 | 0.66 | 6.02 | 5.89 | 0.73 | 0.43 |
1051| 0 | 128 | 466 | 0 | 0 | 0 | 400 | 414 | 0.7 | 6.87 | 6.71 | 0.72 | 0.44 |
1052| 0 | 129 | 504 | 0 | 0 | 0 | 421 | 440 | 0.71 | 6.94 | 6.86 | 0.72 | 0.44 |
1053| 0 | 130 | 501 | 0 | 0 | 0 | 414 | 430 | 0.71 | 5.99 | 5.99 | 0.73 | 0.42 |
1054| 0 | 131 | 531 | 0 | 0 | 0 | 452 | 469 | 0.72 | 7.02 | 7.06 | 0.73 | 0.41 |
1055| 0 | 132 | 532 | 0 | 0 | 0 | 454 | 474 | 0.69 | 6.7 | 6.72 | 0.71 | 0.45 |
1056| 0 | 133 | 504 | 0 | 0 | 0 | 424 | 447 | 0.81 | 8.6 | 8.4 | 0.74 | 0.38 |
1057| 0 | 134 | 504 | 0 | 0 | 0 | 428 | 450 | 0.68 | 6.5 | 6.31 | 0.72 | 0.45 |
1058| 0 | 135 | 510 | 0 | 0 | 0 | 425 | 445 | 0.72 | 7.34 | 7.22 | 0.73 | 0.41 |
1059| 0 | 136 | 487 | 0 | 0 | 0 | 413 | 431 | 0.74 | 7.1 | 7.12 | 0.72 | 0.44 |
1060| 0 | 137 | 530 | 0 | 0 | 0 | 462 | 480 | 0.71 | 5.97 | 5.8 | 0.72 | 0.44 |
1061| 0 | 138 | 495 | 0 | 0 | 0 | 419 | 446 | 0.74 | 7.7 | 7.53 | 0.73 | 0.42 |
1062| 0 | 139 | 512 | 0 | 0 | 0 | 447 | 461 | 0.7 | 6.05 | 6.1 | 0.72 | 0.43 |
1063| 0 | 140 | 534 | 0 | 0 | 0 | 445 | 471 | 0.69 | 6.46 | 6.42 | 0.72 | 0.46 |
1064| 0 | 141 | 508 | 0 | 0 | 0 | 436 | 462 | 0.78 | 7.43 | 7.33 | 0.74 | 0.43 |
1065| 0 | 142 | 501 | 0 | 0 | 0 | 430 | 451 | 0.73 | 6.64 | 6.71 | 0.73 | 0.44 |
1066| 0 | 143 | 485 | 0 | 0 | 0 | 403 | 415 | 0.73 | 6.64 | 6.67 | 0.72 | 0.43 |
1067| 0 | 144 | 488 | 0 | 0 | 0 | 418 | 433 | 0.77 | 7.09 | 6.98 | 0.74 | 0.39 |
1068| 0 | 145 | 548 | 0 | 0 | 0 | 451 | 477 | 0.72 | 6.78 | 6.84 | 0.72 | 0.44 |
1069| 0 | 146 | 507 | 0 | 0 | 0 | 438 | 456 | 0.76 | 8.64 | 8.45 | 0.72 | 0.41 |
1070| 0 | 147 | 507 | 0 | 0 | 0 | 432 | 456 | 0.74 | 6.99 | 6.87 | 0.73 | 0.42 |
1071| 0 | 148 | 534 | 2 | 0 | 0 | 450 | 462 | 0.81 | 8.78 | 8.76 | 0.74 | 0.43 |
1072| 0 | 149 | 506 | 0 | 0 | 0 | 439 | 451 | 0.76 | 7.61 | 7.55 | 0.73 | 0.43 |
1073| 0 | 150 | 493 | 0 | 0 | 0 | 415 | 436 | 0.77 | 6.93 | 6.79 | 0.73 | 0.42 |
1074| 0 | 151 | 491 | 2 | 0 | 0 | 424 | 440 | 0.71 | 6.55 | 6.38 | 0.72 | 0.45 |
1075| 0 | 152 | 514 | 0 | 0 | 0 | 457 | 472 | 0.7 | 5.97 | 5.89 | 0.72 | 0.44 |
1076| 0 | 153 | 516 | 0 | 0 | 0 | 432 | 443 | 0.79 | 7.12 | 7.11 | 0.72 | 0.43 |
1077| 0 | 154 | 542 | 0 | 0 | 0 | 455 | 468 | 0.76 | 6.61 | 6.74 | 0.73 | 0.42 |
1078| 0 | 155 | 491 | 0 | 0 | 0 | 425 | 440 | 0.78 | 7.51 | 7.43 | 0.74 | 0.41 |
1079| 0 | 156 | 485 | 2 | 0 | 0 | 420 | 437 | 0.77 | 7.1 | 7.03 | 0.72 | 0.43 |
1080| 0 | 157 | 512 | 0 | 0 | 0 | 418 | 437 | 0.79 | 7.46 | 7.31 | 0.74 | 0.4 |
1081| 0 | 158 | 515 | 0 | 0 | 0 | 446 | 469 | 0.82 | 8.05 | 8.04 | 0.73 | 0.41 |
1082| 0 | 159 | 527 | 0 | 0 | 0 | 451 | 471 | 0.76 | 7.04 | 6.88 | 0.72 | 0.44 |
1083| 0 | 160 | 510 | 0 | 0 | 0 | 419 | 439 | 0.79 | 7.31 | 7.29 | 0.72 | 0.44 |
1084| 0 | 161 | 505 | 0 | 0 | 0 | 424 | 445 | 0.77 | 6.53 | 6.5 | 0.73 | 0.42 |
1085| 0 | 162 | 501 | 0 | 0 | 0 | 424 | 442 | 0.78 | 6.89 | 6.9 | 0.74 | 0.41 |
1086| 0 | 163 | 486 | 0 | 0 | 0 | 415 | 434 | 0.78 | 7.05 | 6.91 | 0.73 | 0.42 |
1087| 0 | 164 | 530 | 0 | 0 | 0 | 448 | 470 | 0.8 | 6.37 | 6.19 | 0.73 | 0.43 |
1088| 0 | 165 | 520 | 0 | 0 | 0 | 456 | 473 | 0.79 | 6.89 | 6.78 | 0.73 | 0.41 |
1089| 0 | 166 | 524 | 0 | 0 | 0 | 442 | 463 | 0.82 | 7.21 | 7.36 | 0.74 | 0.44 |
1090| 0 | 167 | 483 | 4 | 0 | 0 | 428 | 439 | 0.74 | 6.31 | 6.25 | 0.73 | 0.42 |
1091| 0 | 168 | 496 | 0 | 0 | 0 | 417 | 433 | 0.85 | 6.96 | 6.84 | 0.74 | 0.42 |
1092| 0 | 169 | 515 | 0 | 0 | 0 | 441 | 452 | 0.84 | 7.37 | 7.6 | 0.74 | 0.43 |
1093| 0 | 170 | 511 | 0 | 0 | 0 | 436 | 456 | 0.74 | 6.43 | 6.42 | 0.72 | 0.45 |
1094| 0 | 171 | 522 | 0 | 0 | 0 | 446 | 462 | 0.85 | 6.91 | 6.91 | 0.74 | 0.4 |
1095| 0 | 172 | 505 | 0 | 0 | 0 | 435 | 454 | 0.86 | 7.82 | 7.75 | 0.75 | 0.4 |
1096| 0 | 173 | 518 | 0 | 0 | 0 | 436 | 455 | 0.82 | 6.65 | 6.59 | 0.73 | 0.43 |
1097| 0 | 174 | 481 | 0 | 0 | 0 | 412 | 423 | 0.87 | 7.65 | 7.68 | 0.75 | 0.39 |
1098| 0 | 175 | 513 | 2 | 0 | 0 | 432 | 452 | 0.8 | 6.5 | 6.97 | 0.73 | 0.41 |
1099| 0 | 176 | 511 | 2 | 0 | 0 | 439 | 456 | 0.9 | 8.06 | 7.97 | 0.74 | 0.4 |
1100| 0 | 177 | 503 | 2 | 0 | 0 | 430 | 443 | 0.78 | 6.37 | 6.34 | 0.74 | 0.44 |
1101| 0 | 178 | 510 | 0 | 0 | 0 | 442 | 456 | 0.82 | 7.18 | 7.03 | 0.74 | 0.42 |
1102| 0 | 179 | 511 | 0 | 0 | 0 | 438 | 450 | 0.84 | 7.63 | 7.57 | 0.73 | 0.43 |
1103| 0 | 180 | 497 | 0 | 0 | 0 | 423 | 440 | 0.88 | 6.86 | 6.75 | 0.74 | 0.43 |
1104| 0 | 181 | 507 | 7 | 0 | 0 | 437 | 455 | 0.91 | 7.12 | 7.22 | 0.74 | 0.39 |
1105| 0 | 182 | 526 | 22 | 0 | 0 | 458 | 479 | 0.85 | 7.11 | 7.09 | 0.74 | 0.41 |
1106| 0 | 183 | 488 | 4 | 0 | 0 | 424 | 436 | 0.79 | 6.41 | 6.39 | 0.73 | 0.43 |
1107| 0 | 184 | 499 | 2 | 0 | 0 | 427 | 437 | 0.89 | 6.82 | 6.79 | 0.75 | 0.41 |
1108| 0 | 185 | 531 | 6 | 0 | 0 | 452 | 468 | 0.89 | 6.82 | 6.72 | 0.74 | 0.4 |
1109| 0 | 186 | 483 | 2 | 0 | 0 | 400 | 426 | 0.9 | 6.94 | 6.81 | 0.73 | 0.43 |
1110| 0 | 187 | 532 | 0 | 0 | 0 | 456 | 471 | 0.81 | 5.94 | 6.09 | 0.74 | 0.41 |
1111| 0 | 188 | 467 | 2 | 0 | 0 | 399 | 419 | 0.87 | 6.61 | 6.62 | 0.73 | 0.41 |
1112| 0 | 189 | 533 | 0 | 0 | 0 | 451 | 469 | 0.92 | 7.84 | 7.8 | 0.75 | 0.4 |
1113| 0 | 190 | 513 | 0 | 0 | 0 | 425 | 448 | 0.92 | 8.18 | 8.21 | 0.74 | 0.42 |
1114| 0 | 191 | 492 | 0 | 0 | 0 | 431 | 446 | 0.97 | 7.01 | 7.13 | 0.74 | 0.42 |
1115| 0 | 192 | 546 | 2 | 0 | 0 | 464 | 486 | 0.91 | 7.17 | 7.11 | 0.75 | 0.43 |
1116| 0 | 193 | 490 | 0 | 0 | 0 | 419 | 431 | 0.87 | 6.53 | 6.45 | 0.75 | 0.4 |
1117| 0 | 194 | 502 | 0 | 0 | 0 | 420 | 443 | 0.88 | 7.04 | 6.77 | 0.75 | 0.4 |
1118| 0 | 195 | 518 | 0 | 0 | 0 | 444 | 464 | 0.99 | 7.89 | 7.76 | 0.76 | 0.42 |
1119| 0 | 196 | 517 | 0 | 0 | 0 | 450 | 465 | 1.01 | 8.42 | 8.42 | 0.75 | 0.41 |
1120| 0 | 197 | 493 | 0 | 0 | 0 | 423 | 438 | 1.02 | 8.38 | 8.29 | 0.75 | 0.42 |
1121| 0 | 198 | 504 | 0 | 0 | 0 | 416 | 445 | 0.85 | 6.65 | 6.54 | 0.74 | 0.44 |
1122| 0 | 199 | 522 | 2 | 0 | 0 | 447 | 467 | 0.94 | 6.93 | 7.13 | 0.75 | 0.42 |
1123| 0 | 200 | 497 | 0 | 0 | 0 | 423 | 439 | 0.97 | 7.77 | 7.68 | 0.75 | 0.4 |
1124| 0 | 201 | 505 | 0 | 0 | 0 | 432 | 452 | 0.93 | 6.15 | 6.12 | 0.75 | 0.4 |
1125| 0 | 202 | 531 | 0 | 0 | 0 | 463 | 480 | 1.01 | 7.61 | 7.5 | 0.76 | 0.39 |
1126| 0 | 203 | 504 | 0 | 0 | 0 | 420 | 435 | 1.03 | 7.86 | 7.78 | 0.75 | 0.39 |
1127| 0 | 204 | 518 | 0 | 0 | 0 | 437 | 461 | 0.99 | 7.43 | 7.46 | 0.75 | 0.42 |
1128| 0 | 205 | 483 | 0 | 0 | 0 | 417 | 435 | 0.96 | 6.92 | 6.66 | 0.75 | 0.39 |
1129| 0 | 206 | 531 | 0 | 0 | 0 | 455 | 477 | 0.95 | 6.58 | 6.41 | 0.76 | 0.4 |
1130| 0 | 207 | 484 | 0 | 0 | 0 | 420 | 433 | 1.02 | 7.69 | 7.46 | 0.76 | 0.39 |
1131| 0 | 208 | 518 | 0 | 0 | 0 | 442 | 460 | 1.03 | 7.51 | 7.29 | 0.76 | 0.41 |
1132| 0 | 209 | 505 | 0 | 0 | 0 | 423 | 439 | 1 | 7.68 | 7.45 | 0.76 | 0.4 |
1133| 0 | 210 | 517 | 0 | 0 | 0 | 437 | 455 | 1.14 | 8.62 | 8.43 | 0.77 | 0.4 |
1134| 0 | 211 | 502 | 0 | 0 | 0 | 431 | 442 | 1.03 | 6.57 | 6.47 | 0.76 | 0.41 |
1135| 0 | 212 | 515 | 0 | 0 | 0 | 443 | 459 | 1.02 | 6.72 | 6.81 | 0.76 | 0.4 |
1136| 0 | 213 | 515 | 0 | 0 | 0 | 437 | 455 | 1.12 | 7.76 | 7.57 | 0.77 | 0.42 |
1137| 0 | 214 | 487 | 0 | 0 | 0 | 409 | 429 | 0.98 | 6.34 | 6.21 | 0.76 | 0.42 |
1138| 0 | 215 | 501 | 0 | 0 | 0 | 434 | 448 | 1.15 | 7.77 | 7.73 | 0.76 | 0.4 |
1139| 0 | 216 | 522 | 0 | 0 | 0 | 447 | 466 | 1.07 | 7.2 | 7.13 | 0.77 | 0.43 |
1140| 0 | 217 | 512 | 0 | 0 | 0 | 442 | 459 | 1.13 | 7.18 | 7.68 | 0.77 | 0.42 |
1141| 0 | 218 | 498 | 0 | 0 | 0 | 417 | 436 | 1.08 | 7.1 | 6.96 | 0.76 | 0.39 |
1142| 0 | 219 | 533 | 0 | 0 | 0 | 467 | 483 | 1.11 | 6.35 | 6.25 | 0.77 | 0.39 |
1143| 0 | 220 | 500 | 0 | 0 | 0 | 414 | 437 | 1.13 | 7.55 | 7.39 | 0.77 | 0.4 |
1144| 0 | 221 | 524 | 0 | 0 | 0 | 454 | 475 | 1.13 | 7 | 6.92 | 0.77 | 0.4 |
1145| 0 | 222 | 493 | 0 | 0 | 0 | 411 | 434 | 1.22 | 8.55 | 8.28 | 0.77 | 0.4 |
1146| 0 | 223 | 511 | 0 | 0 | 0 | 448 | 459 | 1.17 | 7.64 | 7.52 | 0.78 | 0.41 |
1147| 0 | 224 | 514 | 0 | 0 | 0 | 428 | 451 | 1.2 | 7.6 | 7.63 | 0.77 | 0.4 |
1148| 0 | 225 | 504 | 0 | 0 | 0 | 446 | 454 | 1.27 | 6.86 | 6.81 | 0.78 | 0.39 |
1149| 0 | 226 | 503 | 0 | 0 | 0 | 413 | 439 | 1.14 | 6.3 | 6.36 | 0.77 | 0.41 |
1150| 0 | 227 | 495 | 0 | 0 | 0 | 417 | 444 | 1.28 | 7.8 | 7.62 | 0.78 | 0.38 |
1151| 0 | 228 | 525 | 0 | 0 | 0 | 451 | 464 | 1.24 | 8.64 | 8.57 | 0.78 | 0.39 |
1152| 0 | 229 | 506 | 0 | 0 | 0 | 452 | 464 | 1.28 | 8.21 | 8.1 | 0.78 | 0.41 |
1153| 0 | 230 | 510 | 0 | 0 | 0 | 450 | 470 | 1.25 | 7.31 | 7.21 | 0.78 | 0.39 |
1154| 0 | 231 | 515 | 0 | 0 | 0 | 427 | 448 | 1.3 | 7.6 | 7.33 | 0.79 | 0.4 |
1155| 0 | 232 | 498 | 0 | 0 | 0 | 419 | 443 | 1.28 | 7.56 | 7.29 | 0.79 | 0.4 |
1156| 0 | 233 | 507 | 0 | 0 | 0 | 428 | 446 | 1.32 | 7.48 | 7.47 | 0.78 | 0.41 |
1157| 0 | 234 | 509 | 0 | 0 | 0 | 431 | 450 | 1.29 | 8.19 | 8.15 | 0.79 | 0.39 |
1158| 0 | 235 | 535 | 0 | 0 | 0 | 450 | 467 | 1.33 | 7.1 | 7.01 | 0.78 | 0.41 |
1159| 0 | 236 | 499 | 0 | 0 | 0 | 428 | 446 | 1.26 | 6.55 | 6.55 | 0.78 | 0.41 |
1160| 0 | 237 | 493 | 0 | 0 | 0 | 429 | 449 | 1.45 | 9.6 | 9.51 | 0.79 | 0.4 |
1161| 0 | 238 | 496 | 0 | 0 | 0 | 423 | 441 | 1.43 | 8.94 | 8.91 | 0.79 | 0.38 |
1162| 0 | 239 | 506 | 0 | 0 | 0 | 433 | 452 | 1.31 | 5.98 | 5.99 | 0.79 | 0.38 |
1163| 0 | 240 | 534 | 0 | 0 | 0 | 462 | 479 | 1.33 | 8.23 | 8.12 | 0.79 | 0.39 |
1164| 0 | 241 | 526 | 0 | 0 | 0 | 448 | 473 | 1.45 | 9.04 | 8.78 | 0.79 | 0.39 |
1165| 0 | 242 | 486 | 0 | 0 | 0 | 411 | 429 | 1.33 | 7.98 | 7.8 | 0.79 | 0.39 |
1166| 0 | 243 | 505 | 0 | 0 | 0 | 432 | 453 | 1.46 | 8.65 | 8.62 | 0.8 | 0.38 |
1167| 0 | 244 | 532 | 0 | 0 | 0 | 445 | 458 | 1.36 | 7.52 | 7.33 | 0.79 | 0.4 |
1168| 0 | 245 | 491 | 0 | 0 | 0 | 426 | 438 | 1.44 | 6.72 | 6.74 | 0.8 | 0.38 |
1169| 0 | 246 | 534 | 0 | 0 | 0 | 443 | 465 | 1.38 | 7.14 | 7.08 | 0.79 | 0.4 |
1170| 0 | 247 | 495 | 0 | 0 | 0 | 411 | 433 | 1.4 | 8.29 | 8.19 | 0.79 | 0.39 |
1171| 0 | 248 | 514 | 0 | 0 | 0 | 438 | 450 | 1.36 | 7.98 | 7.85 | 0.8 | 0.39 |
1172| 0 | 249 | 522 | 0 | 0 | 0 | 439 | 463 | 1.51 | 8.71 | 8.6 | 0.8 | 0.38 |
1173| 0 | 250 | 505 | 0 | 0 | 0 | 434 | 452 | 1.37 | 8.34 | 8.06 | 0.79 | 0.39 |
1174| 0 | 251 | 511 | 0 | 0 | 0 | 437 | 453 | 1.41 | 7.83 | 7.66 | 0.8 | 0.39 |
1175| 0 | 252 | 499 | 0 | 0 | 0 | 417 | 438 | 1.38 | 7.04 | 6.99 | 0.8 | 0.38 |
1176| 0 | 253 | 491 | 0 | 0 | 0 | 415 | 438 | 1.35 | 7.17 | 7.01 | 0.79 | 0.38 |
1177| 0 | 254 | 523 | 0 | 0 | 0 | 449 | 466 | 1.44 | 8.05 | 8.01 | 0.79 | 0.38 |
1178| 0 | 255 | 479 | 0 | 0 | 0 | 407 | 425 | 1.36 | 7.11 | 7.03 | 0.79 | 0.39 |
1179| 0 | 256 | 539 | 0 | 0 | 0 | 445 | 461 | 1.37 | 7.74 | 7.61 | 0.79 | 0.38 |
1180| 0 | 257 | 516 | 0 | 0 | 0 | 442 | 462 | 1.42 | 9.17 | 8.87 | 0.79 | 0.37 |
1181| 0 | 258 | 503 | 0 | 0 | 0 | 432 | 447 | 1.28 | 6.24 | 6.21 | 0.79 | 0.39 |
1182| 0 | 259 | 544 | 0 | 0 | 0 | 461 | 481 | 1.38 | 8.29 | 8.04 | 0.79 | 0.39 |
1183| 0 | 260 | 492 | 0 | 0 | 0 | 417 | 438 | 1.33 | 7.53 | 7.43 | 0.78 | 0.41 |
1184| 0 | 261 | 484 | 0 | 0 | 0 | 419 | 441 | 1.34 | 7.69 | 7.65 | 0.79 | 0.39 |
1185| 0 | 262 | 515 | 0 | 0 | 0 | 429 | 446 | 1.27 | 6.56 | 6.45 | 0.79 | 0.39 |
1186| 0 | 263 | 522 | 0 | 0 | 0 | 436 | 453 | 1.27 | 6.96 | 6.78 | 0.78 | 0.39 |
1187| 0 | 264 | 487 | 0 | 0 | 0 | 399 | 425 | 1.3 | 8.88 | 8.73 | 0.78 | 0.39 |
1188| 0 | 265 | 509 | 0 | 0 | 0 | 443 | 461 | 1.16 | 7.6 | 7.64 | 0.78 | 0.39 |
1189| 0 | 266 | 511 | 0 | 0 | 0 | 439 | 457 | 1.35 | 7.61 | 7.39 | 0.79 | 0.39 |
1190| 0 | 267 | 510 | 0 | 0 | 0 | 439 | 460 | 1.33 | 7.77 | 7.82 | 0.79 | 0.37 |
1191| 0 | 268 | 557 | 0 | 0 | 0 | 481 | 497 | 1.27 | 9.26 | 9.01 | 0.78 | 0.38 |
1192| 0 | 269 | 498 | 0 | 0 | 0 | 412 | 433 | 1.24 | 8.45 | 8.13 | 0.78 | 0.4 |
1193| 0 | 270 | 515 | 0 | 0 | 0 | 437 | 453 | 1.3 | 7.9 | 7.78 | 0.79 | 0.39 |
1194| 0 | 271 | 516 | 0 | 0 | 0 | 444 | 464 | 1.07 | 6.64 | 6.5 | 0.78 | 0.4 |
1195| 0 | 272 | 503 | 0 | 0 | 0 | 429 | 448 | 1.16 | 8.3 | 8.15 | 0.78 | 0.39 |
1196| 0 | 273 | 472 | 0 | 0 | 0 | 401 | 422 | 1.13 | 7.71 | 7.51 | 0.77 | 0.41 |
1197| 0 | 274 | 539 | 0 | 0 | 0 | 461 | 474 | 1.24 | 8.99 | 8.98 | 0.78 | 0.4 |
1198| 0 | 275 | 487 | 0 | 0 | 0 | 407 | 432 | 1.21 | 9.11 | 8.78 | 0.78 | 0.39 |
1199| 0 | 276 | 510 | 0 | 0 | 0 | 432 | 454 | 1.1 | 7.58 | 7.34 | 0.76 | 0.39 |
1200| 0 | 277 | 521 | 0 | 0 | 0 | 452 | 465 | 1.08 | 7.52 | 7.36 | 0.76 | 0.41 |
1201| 0 | 278 | 493 | 0 | 0 | 0 | 399 | 421 | 1.06 | 7.72 | 7.61 | 0.77 | 0.42 |
1202| 0 | 279 | 540 | 0 | 0 | 0 | 468 | 486 | 1.09 | 7.36 | 7.24 | 0.76 | 0.39 |
1203| 0 | 280 | 503 | 0 | 0 | 0 | 435 | 447 | 1.24 | 8.78 | 8.71 | 0.78 | 0.39 |
1204| 0 | 281 | 486 | 0 | 0 | 0 | 430 | 445 | 1.02 | 7.22 | 7.23 | 0.76 | 0.41 |
1205| 0 | 282 | 514 | 0 | 0 | 0 | 436 | 451 | 1.02 | 7.75 | 7.56 | 0.76 | 0.4 |
1206| 0 | 283 | 509 | 0 | 0 | 0 | 426 | 447 | 1.05 | 7.14 | 7.03 | 0.76 | 0.41 |
1207| 0 | 284 | 522 | 0 | 0 | 0 | 461 | 473 | 1.06 | 6.56 | 6.63 | 0.76 | 0.4 |
1208| 0 | 285 | 500 | 0 | 0 | 0 | 424 | 441 | 1.11 | 7.37 | 7.34 | 0.77 | 0.4 |
1209| 0 | 286 | 505 | 0 | 0 | 0 | 428 | 445 | 1.01 | 6.49 | 6.34 | 0.76 | 0.4 |
1210| 0 | 287 | 525 | 0 | 0 | 0 | 444 | 463 | 0.97 | 7.73 | 7.6 | 0.75 | 0.42 |
1211| 0 | 288 | 495 | 0 | 0 | 0 | 416 | 437 | 0.95 | 6.38 | 6.38 | 0.75 | 0.41 |
1212| 0 | 289 | 523 | 0 | 0 | 0 | 451 | 465 | 0.98 | 7.76 | 7.59 | 0.75 | 0.41 |
1213| 0 | 290 | 495 | 0 | 0 | 0 | 426 | 438 | 1.07 | 7.72 | 7.68 | 0.77 | 0.38 |
1214| 0 | 291 | 536 | 0 | 0 | 0 | 464 | 489 | 1.04 | 8.22 | 8.29 | 0.76 | 0.39 |
1215| 0 | 292 | 493 | 0 | 0 | 0 | 412 | 435 | 0.94 | 7.92 | 7.89 | 0.74 | 0.43 |
1216| 0 | 293 | 517 | 0 | 0 | 0 | 439 | 461 | 0.98 | 7.36 | 7.25 | 0.75 | 0.39 |
1217| 0 | 294 | 501 | 0 | 0 | 0 | 419 | 439 | 0.95 | 6.78 | 6.62 | 0.76 | 0.4 |
1218| 0 | 295 | 511 | 0 | 0 | 0 | 428 | 446 | 0.94 | 7.23 | 7.04 | 0.75 | 0.41 |
1219| 0 | 296 | 486 | 0 | 0 | 0 | 419 | 437 | 0.97 | 8.03 | 7.74 | 0.74 | 0.41 |
1220| 0 | 297 | 533 | 0 | 0 | 0 | 439 | 464 | 0.91 | 6.7 | 6.53 | 0.75 | 0.4 |
1221| 0 | 298 | 508 | 0 | 0 | 0 | 422 | 443 | 0.99 | 8.03 | 7.79 | 0.75 | 0.39 |
1222| 0 | 299 | 519 | 0 | 0 | 0 | 447 | 464 | 0.94 | 8.62 | 8.39 | 0.75 | 0.4 |
1223| 0 | 300 | 475 | 0 | 0 | 0 | 396 | 411 | 0.92 | 8.62 | 8.49 | 0.75 | 0.4 |
1224| 0 | 301 | 541 | 0 | 0 | 0 | 471 | 484 | 0.94 | 7.94 | 7.79 | 0.75 | 0.39 |
1225| 0 | 302 | 515 | 0 | 0 | 0 | 433 | 451 | 0.81 | 6.59 | 6.4 | 0.74 | 0.41 |
1226| 0 | 303 | 530 | 0 | 0 | 0 | 455 | 468 | 0.96 | 8.21 | 8.08 | 0.74 | 0.42 |
1227| 0 | 304 | 476 | 0 | 0 | 0 | 397 | 410 | 0.88 | 6.97 | 7.07 | 0.73 | 0.42 |
1228| 0 | 305 | 536 | 0 | 0 | 0 | 448 | 463 | 0.93 | 6.63 | 6.57 | 0.74 | 0.43 |
1229| 0 | 306 | 494 | 0 | 0 | 0 | 424 | 440 | 0.84 | 6.53 | 6.45 | 0.74 | 0.43 |
1230| 0 | 307 | 502 | 0 | 0 | 0 | 439 | 453 | 0.88 | 6.97 | 6.88 | 0.74 | 0.4 |
1231| 0 | 308 | 498 | 0 | 0 | 0 | 424 | 440 | 0.92 | 7.76 | 7.61 | 0.74 | 0.42 |
1232| 0 | 309 | 541 | 0 | 0 | 0 | 454 | 468 | 0.83 | 7.05 | 7.02 | 0.73 | 0.42 |
1233| 0 | 310 | 508 | 0 | 0 | 0 | 433 | 454 | 0.86 | 6.84 | 6.69 | 0.73 | 0.41 |
1234| 0 | 311 | 484 | 0 | 0 | 0 | 406 | 426 | 0.88 | 8.21 | 7.98 | 0.73 | 0.43 |
1235| 0 | 312 | 508 | 0 | 0 | 0 | 450 | 470 | 0.85 | 7.15 | 6.85 | 0.73 | 0.4 |
1236| 0 | 313 | 523 | 0 | 0 | 0 | 435 | 454 | 0.9 | 8.06 | 7.83 | 0.74 | 0.42 |
1237| 0 | 314 | 509 | 0 | 0 | 0 | 441 | 457 | 0.85 | 7.51 | 7.35 | 0.74 | 0.41 |
1238| 0 | 315 | 524 | 0 | 0 | 0 | 439 | 462 | 0.78 | 6.07 | 6.11 | 0.72 | 0.43 |
1239| 0 | 316 | 509 | 0 | 0 | 0 | 438 | 456 | 0.77 | 7.84 | 7.57 | 0.72 | 0.42 |
1240| 0 | 317 | 495 | 0 | 0 | 0 | 424 | 442 | 0.85 | 7.01 | 6.92 | 0.73 | 0.41 |
1241| 0 | 318 | 472 | 0 | 0 | 0 | 401 | 415 | 0.92 | 8.64 | 8.46 | 0.73 | 0.4 |
1242| 0 | 319 | 548 | 0 | 0 | 0 | 465 | 490 | 0.81 | 7.2 | 7.05 | 0.73 | 0.41 |
1243| 0 | 320 | 495 | 0 | 0 | 0 | 434 | 446 | 0.81 | 6.64 | 6.53 | 0.73 | 0.42 |
1244| 0 | 321 | 519 | 0 | 0 | 0 | 438 | 459 | 0.82 | 6.93 | 6.74 | 0.73 | 0.44 |
1245| 0 | 322 | 498 | 0 | 0 | 0 | 424 | 443 | 0.78 | 7.17 | 7.02 | 0.72 | 0.45 |
1246| 0 | 323 | 535 | 0 | 0 | 0 | 445 | 468 | 0.72 | 5.91 | 5.82 | 0.72 | 0.47 |
1247| 0 | 324 | 482 | 0 | 0 | 0 | 413 | 431 | 0.88 | 8.75 | 8.47 | 0.74 | 0.42 |
1248| 0 | 325 | 528 | 0 | 0 | 0 | 449 | 467 | 0.88 | 8.04 | 7.88 | 0.74 | 0.41 |
1249| 0 | 326 | 503 | 0 | 0 | 0 | 430 | 450 | 0.81 | 7.57 | 7.48 | 0.72 | 0.44 |
1250| 0 | 327 | 489 | 0 | 0 | 0 | 411 | 428 | 0.79 | 7.53 | 7.3 | 0.72 | 0.43 |
1251| 0 | 328 | 533 | 0 | 0 | 0 | 459 | 475 | 0.75 | 7.12 | 7.03 | 0.72 | 0.42 |
1252| 0 | 329 | 516 | 0 | 0 | 0 | 430 | 451 | 0.75 | 6.7 | 6.56 | 0.71 | 0.44 |
1253| 0 | 330 | 530 | 0 | 0 | 0 | 455 | 475 | 0.83 | 7.21 | 7.22 | 0.73 | 0.45 |
1254| 0 | 331 | 495 | 0 | 0 | 0 | 420 | 442 | 0.8 | 7.51 | 7.46 | 0.72 | 0.44 |
1255| 0 | 332 | 493 | 0 | 0 | 0 | 417 | 435 | 0.76 | 6.15 | 6.15 | 0.72 | 0.43 |
1256| 0 | 333 | 498 | 0 | 0 | 0 | 424 | 444 | 0.76 | 6.93 | 6.85 | 0.72 | 0.43 |
1257| 0 | 334 | 513 | 0 | 0 | 0 | 451 | 467 | 0.8 | 7.51 | 7.32 | 0.72 | 0.45 |
1258| 0 | 335 | 502 | 0 | 0 | 0 | 413 | 427 | 0.72 | 6.94 | 6.9 | 0.71 | 0.44 |
1259| 0 | 336 | 531 | 0 | 0 | 0 | 457 | 471 | 0.67 | 5.65 | 5.51 | 0.71 | 0.46 |
1260| 0 | 337 | 518 | 0 | 0 | 0 | 426 | 451 | 0.8 | 7.6 | 7.36 | 0.72 | 0.45 |
1261| 0 | 338 | 498 | 0 | 0 | 0 | 427 | 448 | 0.75 | 6.76 | 6.54 | 0.72 | 0.41 |
1262| 0 | 339 | 522 | 0 | 0 | 0 | 429 | 456 | 0.78 | 7.51 | 7.18 | 0.72 | 0.45 |
1263| 0 | 340 | 485 | 0 | 0 | 0 | 419 | 435 | 0.79 | 7.19 | 7.19 | 0.72 | 0.42 |
1264| 0 | 341 | 523 | 0 | 0 | 0 | 447 | 471 | 0.79 | 7.12 | 7.1 | 0.73 | 0.4 |
1265| 0 | 342 | 490 | 0 | 0 | 0 | 424 | 449 | 0.71 | 5.88 | 5.91 | 0.71 | 0.47 |
1266| 0 | 343 | 532 | 0 | 0 | 0 | 450 | 471 | 0.7 | 6.13 | 5.93 | 0.72 | 0.42 |
1267| 0 | 344 | 497 | 0 | 0 | 0 | 423 | 444 | 0.7 | 6.09 | 6.05 | 0.71 | 0.45 |
1268| 0 | 345 | 519 | 0 | 0 | 0 | 450 | 467 | 0.8 | 7.29 | 7.26 | 0.72 | 0.44 |
1269| 0 | 346 | 488 | 0 | 0 | 0 | 406 | 420 | 0.69 | 6.22 | 6.08 | 0.7 | 0.47 |
1270| 0 | 347 | 537 | 0 | 0 | 0 | 450 | 465 | 0.74 | 6.51 | 6.46 | 0.71 | 0.43 |
1271| 0 | 348 | 492 | 0 | 0 | 0 | 420 | 436 | 0.77 | 7.54 | 7.39 | 0.73 | 0.41 |
1272| 0 | 349 | 509 | 0 | 0 | 0 | 430 | 457 | 0.73 | 6.92 | 6.7 | 0.72 | 0.42 |
1273| 0 | 350 | 514 | 0 | 0 | 0 | 416 | 442 | 0.67 | 6.74 | 6.54 | 0.71 | 0.47 |
1274| 0 | 351 | 525 | 0 | 0 | 0 | 458 | 476 | 0.78 | 6.98 | 6.89 | 0.72 | 0.44 |
1275| 0 | 352 | 505 | 0 | 0 | 0 | 429 | 444 | 0.75 | 7.12 | 6.99 | 0.72 | 0.44 |
1276| 0 | 353 | 477 | 0 | 0 | 0 | 404 | 419 | 0.7 | 6.36 | 6.55 | 0.71 | 0.44 |
1277| 0 | 354 | 516 | 0 | 0 | 0 | 450 | 469 | 0.74 | 7.63 | 7.4 | 0.72 | 0.44 |
1278| 0 | 355 | 530 | 0 | 0 | 0 | 451 | 473 | 0.66 | 5.61 | 5.71 | 0.71 | 0.46 |
1279| 0 | 356 | 511 | 2 | 0 | 0 | 442 | 466 | 0.71 | 6.76 | 6.69 | 0.71 | 0.44 |
1280| 0 | 357 | 499 | 2 | 0 | 0 | 417 | 439 | 0.73 | 7.34 | 7.07 | 0.72 | 0.42 |
1281| 0 | 358 | 543 | 0 | 0 | 0 | 463 | 487 | 0.66 | 5.94 | 5.73 | 0.7 | 0.44 |
1282| 0 | 359 | 472 | 0 | 0 | 0 | 403 | 416 | 0.72 | 6.48 | 6.42 | 0.71 | 0.48 |
1283| 0 | 360 | 489 | 4 | 0 | 0 | 423 | 436 | 0.75 | 7.77 | 7.67 | 0.73 | 0.41 |
1284| 0 | 361 | 536 | 17 | 0 | 0 | 468 | 489 | 0.77 | 8.47 | 8.86 | 0.72 | 0.43 |
1285| 0 | 362 | 478 | 15 | 0 | 0 | 412 | 428 | 0.75 | 6.49 | 6.55 | 0.72 | 0.44 |
1286| 0 | 363 | 488 | 20 | 0 | 0 | 430 | 448 | 0.69 | 6.74 | 6.8 | 0.7 | 0.46 |
1287| 0 | 364 | 510 | 0 | 0 | 0 | 442 | 458 | 0.66 | 5.98 | 5.83 | 0.72 | 0.43 |
1288| 0 | 365 | 512 | 0 | 0 | 0 | 446 | 459 | 0.72 | 7.67 | 7.49 | 0.73 | 0.42 |
1289| 0 | 366 | 516 | 0 | 0 | 0 | 420 | 442 | 0.66 | 6.36 | 6.19 | 0.7 | 0.42 |
1290| 0 | 367 | 542 | 2 | 0 | 0 | 468 | 483 | 0.73 | 7.81 | 7.7 | 0.71 | 0.45 |
1291| 0 | 368 | 540 | 0 | 0 | 0 | 470 | 479 | 0.69 | 8.05 | 8 | 0.71 | 0.42 |
1292| 0 | 369 | 521 | 2 | 0 | 0 | 440 | 457 | 0.64 | 6.5 | 6.47 | 0.7 | 0.45 |
1293| 0 | 370 | 473 | 0 | 0 | 0 | 407 | 420 | 0.7 | 7.57 | 7.43 | 0.72 | 0.45 |
1294| 0 | 371 | 460 | 0 | 0 | 0 | 397 | 413 | 0.69 | 5.87 | 5.72 | 0.71 | 0.46 |
1295| 0 | 372 | 524 | 0 | 0 | 0 | 445 | 458 | 0.76 | 7.72 | 7.58 | 0.72 | 0.43 |
1296| 0 | 373 | 503 | 0 | 0 | 0 | 437 | 449 | 0.72 | 7.12 | 6.99 | 0.72 | 0.41 |
1297| 0 | 374 | 507 | 2 | 0 | 0 | 431 | 449 | 0.76 | 8.32 | 8.29 | 0.71 | 0.45 |
1298| 0 | 375 | 500 | 0 | 0 | 0 | 433 | 450 | 0.69 | 6.31 | 6.36 | 0.71 | 0.44 |
1299| 0 | 376 | 508 | 0 | 0 | 0 | 423 | 448 | 0.69 | 6.24 | 6.09 | 0.71 | 0.44 |
1300| 0 | 377 | 525 | 0 | 0 | 0 | 446 | 462 | 0.59 | 5.65 | 5.52 | 0.7 | 0.45 |
1301| 0 | 378 | 513 | 0 | 0 | 0 | 433 | 449 | 0.69 | 6.3 | 6.39 | 0.7 | 0.44 |
1302| 0 | 379 | 513 | 0 | 0 | 0 | 425 | 448 | 0.68 | 5.61 | 5.56 | 0.71 | 0.45 |
1303| 0 | 380 | 535 | 0 | 0 | 0 | 460 | 479 | 0.69 | 6.59 | 6.42 | 0.71 | 0.42 |
1304| 0 | 381 | 526 | 2 | 0 | 0 | 439 | 458 | 0.69 | 7.36 | 7.2 | 0.71 | 0.46 |
1305| 0 | 382 | 520 | 0 | 0 | 0 | 427 | 451 | 0.75 | 7.17 | 7.11 | 0.71 | 0.43 |
1306| 0 | 383 | 490 | 0 | 0 | 0 | 419 | 435 | 0.64 | 6.75 | 6.61 | 0.71 | 0.41 |
1307| 0 | 384 | 501 | 0 | 0 | 0 | 420 | 436 | 0.64 | 6.1 | 5.96 | 0.71 | 0.42 |
1308| 0 | 385 | 501 | 0 | 0 | 0 | 438 | 449 | 0.65 | 6.3 | 6.4 | 0.7 | 0.47 |
1309| 0 | 386 | 497 | 0 | 0 | 0 | 428 | 451 | 0.68 | 7.65 | 7.46 | 0.71 | 0.46 |
1310| 0 | 387 | 525 | 0 | 0 | 0 | 462 | 473 | 0.73 | 7.09 | 7.04 | 0.72 | 0.44 |
1311| 0 | 388 | 499 | 0 | 0 | 0 | 431 | 443 | 0.69 | 7.2 | 7.1 | 0.71 | 0.43 |
1312| 0 | 389 | 528 | 0 | 0 | 0 | 440 | 468 | 0.73 | 8.27 | 8.09 | 0.7 | 0.45 |
1313| 0 | 390 | 488 | 0 | 0 | 0 | 421 | 436 | 0.69 | 6.73 | 6.62 | 0.71 | 0.45 |
1314| 0 | 391 | 526 | 0 | 0 | 0 | 438 | 467 | 0.68 | 6.8 | 6.63 | 0.71 | 0.43 |
1315| 0 | 392 | 522 | 0 | 0 | 0 | 444 | 459 | 0.7 | 6.69 | 6.55 | 0.71 | 0.47 |
1316| 0 | 393 | 490 | 2 | 0 | 0 | 419 | 440 | 0.67 | 6.47 | 6.36 | 0.71 | 0.46 |
1317| 0 | 394 | 541 | 0 | 0 | 0 | 464 | 472 | 0.63 | 6.1 | 6.01 | 0.71 | 0.46 |
1318| 0 | 395 | 496 | 0 | 0 | 0 | 429 | 445 | 0.66 | 6.48 | 6.29 | 0.71 | 0.45 |
1319| 0 | 396 | 496 | 0 | 0 | 0 | 418 | 432 | 0.62 | 6.07 | 5.87 | 0.71 | 0.45 |
1320| 0 | 397 | 523 | 0 | 0 | 0 | 459 | 473 | 0.64 | 5.92 | 5.81 | 0.7 | 0.44 |
1321| 0 | 398 | 497 | 0 | 0 | 0 | 406 | 430 | 0.66 | 6.43 | 6.3 | 0.71 | 0.44 |
1322| 0 | 399 | 506 | 0 | 0 | 0 | 424 | 444 | 0.65 | 6.78 | 6.6 | 0.72 | 0.45 |
1323| 0 | 400 | 519 | 0 | 0 | 0 | 443 | 463 | 0.71 | 7.08 | 6.91 | 0.72 | 0.44 |
1324| 0 | 401 | 502 | 0 | 0 | 0 | 430 | 448 | 0.7 | 6.84 | 6.69 | 0.71 | 0.42 |
1325| 0 | 402 | 504 | 0 | 0 | 0 | 425 | 443 | 0.69 | 6.98 | 6.87 | 0.72 | 0.44 |
1326| 0 | 403 | 504 | 0 | 0 | 0 | 437 | 454 | 0.65 | 6.23 | 6.24 | 0.71 | 0.45 |
1327| 0 | 404 | 509 | 0 | 0 | 0 | 438 | 454 | 0.71 | 7.8 | 7.64 | 0.72 | 0.42 |
1328| 0 | 405 | 518 | 0 | 0 | 0 | 446 | 458 | 0.65 | 6.56 | 6.47 | 0.71 | 0.43 |
1329| 0 | 406 | 492 | 0 | 0 | 0 | 413 | 430 | 0.68 | 6.74 | 6.68 | 0.7 | 0.44 |
1330| 0 | 407 | 530 | 0 | 0 | 0 | 454 | 475 | 0.67 | 6.41 | 6.29 | 0.7 | 0.44 |
1331| 0 | 408 | 488 | 0 | 0 | 0 | 410 | 424 | 0.72 | 7.22 | 7.17 | 0.72 | 0.43 |
1332| 0 | 409 | 541 | 0 | 0 | 0 | 460 | 479 | 0.63 | 6.59 | 6.5 | 0.7 | 0.48 |
1333| 0 | 410 | 481 | 0 | 0 | 0 | 406 | 423 | 0.7 | 6.42 | 6.43 | 0.73 | 0.4 |
1334| 0 | 411 | 540 | 0 | 0 | 0 | 461 | 479 | 0.62 | 6.63 | 6.62 | 0.69 | 0.46 |
1335| 0 | 412 | 478 | 0 | 0 | 0 | 409 | 425 | 0.66 | 6.58 | 6.59 | 0.72 | 0.41 |
1336| 0 | 413 | 542 | 0 | 0 | 0 | 456 | 475 | 0.67 | 7.23 | 7.08 | 0.7 | 0.46 |
1337| 0 | 414 | 494 | 0 | 0 | 0 | 426 | 440 | 0.68 | 7.07 | 7.12 | 0.72 | 0.41 |
1338| 0 | 415 | 522 | 0 | 0 | 0 | 446 | 472 | 0.65 | 5.69 | 5.48 | 0.71 | 0.44 |
1339| 0 | 416 | 494 | 0 | 0 | 0 | 412 | 434 | 0.72 | 6.74 | 6.72 | 0.72 | 0.43 |
1340| 0 | 417 | 530 | 0 | 0 | 0 | 450 | 466 | 0.63 | 5.9 | 5.81 | 0.7 | 0.49 |
1341| 0 | 418 | 500 | 0 | 0 | 0 | 434 | 454 | 0.7 | 6.7 | 6.83 | 0.73 | 0.42 |
1342| 0 | 419 | 534 | 0 | 0 | 0 | 454 | 471 | 0.62 | 6.16 | 6.04 | 0.69 | 0.47 |
1343| 0 | 420 | 484 | 0 | 0 | 0 | 413 | 428 | 0.71 | 7.15 | 7.27 | 0.72 | 0.42 |
1344| 0 | 421 | 535 | 0 | 0 | 0 | 450 | 479 | 0.63 | 5.81 | 5.59 | 0.7 | 0.46 |
1345| 0 | 422 | 495 | 0 | 0 | 0 | 420 | 436 | 0.68 | 6.51 | 6.39 | 0.72 | 0.43 |
1346| 0 | 423 | 509 | 0 | 0 | 0 | 427 | 442 | 0.7 | 6.67 | 6.62 | 0.7 | 0.45 |
1347| 0 | 424 | 518 | 0 | 0 | 0 | 437 | 459 | 0.66 | 7.27 | 7.02 | 0.72 | 0.44 |
1348| 0 | 425 | 491 | 0 | 0 | 0 | 424 | 441 | 0.69 | 6.96 | 6.87 | 0.72 | 0.46 |
1349| 0 | 426 | 530 | 0 | 0 | 0 | 461 | 477 | 0.67 | 6.71 | 6.64 | 0.72 | 0.44 |
1350| 0 | 427 | 503 | 0 | 0 | 0 | 434 | 455 | 0.69 | 6.85 | 6.83 | 0.71 | 0.46 |
1351| 0 | 428 | 499 | 0 | 0 | 0 | 417 | 441 | 0.63 | 6.3 | 6.09 | 0.71 | 0.44 |
1352| 0 | 429 | 501 | 0 | 0 | 0 | 420 | 442 | 0.69 | 6.58 | 6.52 | 0.71 | 0.44 |
1353| 0 | 430 | 506 | 0 | 0 | 0 | 436 | 457 | 0.66 | 5.9 | 5.86 | 0.71 | 0.45 |
1354| 0 | 431 | 531 | 0 | 0 | 0 | 449 | 472 | 0.73 | 8.81 | 8.51 | 0.73 | 0.43 |
1355| 0 | 432 | 480 | 0 | 0 | 0 | 419 | 433 | 0.61 | 6.04 | 5.93 | 0.71 | 0.43 |
1356| 0 | 433 | 525 | 0 | 0 | 0 | 450 | 466 | 0.67 | 6.37 | 6.27 | 0.72 | 0.44 |
1357| 0 | 434 | 522 | 0 | 0 | 0 | 435 | 453 | 0.65 | 6.1 | 6.22 | 0.71 | 0.44 |
1358| 0 | 435 | 487 | 0 | 0 | 0 | 422 | 435 | 0.62 | 5.54 | 5.5 | 0.7 | 0.46 |
1359| 0 | 436 | 521 | 0 | 0 | 0 | 450 | 465 | 0.65 | 6.68 | 6.51 | 0.72 | 0.45 |
1360| 0 | 437 | 497 | 0 | 0 | 0 | 414 | 434 | 0.67 | 6.6 | 6.43 | 0.72 | 0.44 |
1361| 0 | 438 | 521 | 0 | 0 | 0 | 435 | 452 | 0.65 | 6.52 | 6.28 | 0.71 | 0.43 |
1362| 0 | 439 | 528 | 0 | 0 | 0 | 458 | 480 | 0.67 | 6.59 | 6.6 | 0.7 | 0.44 |
1363| 0 | 440 | 504 | 0 | 0 | 0 | 434 | 451 | 0.7 | 7.03 | 6.9 | 0.72 | 0.42 |
1364| 0 | 441 | 511 | 0 | 0 | 0 | 431 | 452 | 0.69 | 6.78 | 6.89 | 0.71 | 0.47 |
1365| 0 | 442 | 507 | 0 | 0 | 0 | 429 | 450 | 0.68 | 6.61 | 6.41 | 0.71 | 0.41 |
1366| 0 | 443 | 507 | 0 | 0 | 0 | 420 | 440 | 0.72 | 6.4 | 6.5 | 0.73 | 0.41 |
1367| 0 | 444 | 514 | 0 | 0 | 0 | 428 | 444 | 0.66 | 6.7 | 6.59 | 0.72 | 0.45 |
1368| 0 | 445 | 487 | 0 | 0 | 0 | 406 | 423 | 0.64 | 6.71 | 6.63 | 0.72 | 0.43 |
1369| 0 | 446 | 511 | 0 | 0 | 0 | 436 | 456 | 0.64 | 6.08 | 5.95 | 0.72 | 0.42 |
1370| 0 | 447 | 480 | 0 | 0 | 0 | 407 | 429 | 0.61 | 6.05 | 5.83 | 0.71 | 0.44 |
1371| 0 | 448 | 548 | 0 | 0 | 0 | 472 | 493 | 0.75 | 8.12 | 7.95 | 0.73 | 0.43 |
1372| 0 | 449 | 499 | 0 | 0 | 0 | 423 | 442 | 0.67 | 5.88 | 6.01 | 0.72 | 0.44 |
1373| 0 | 450 | 495 | 0 | 0 | 0 | 422 | 440 | 0.72 | 6.95 | 6.82 | 0.72 | 0.41 |
1374| 0 | 451 | 537 | 0 | 0 | 0 | 456 | 478 | 0.64 | 6.12 | 6.31 | 0.71 | 0.43 |
1375| 0 | 452 | 526 | 0 | 0 | 0 | 454 | 474 | 0.69 | 7.21 | 7.04 | 0.72 | 0.41 |
1376| 0 | 453 | 522 | 0 | 0 | 0 | 441 | 462 | 0.58 | 5.28 | 5.29 | 0.7 | 0.44 |
1377| 0 | 454 | 503 | 0 | 0 | 0 | 436 | 453 | 0.61 | 5.68 | 5.55 | 0.72 | 0.44 |
1378| 0 | 455 | 517 | 0 | 0 | 0 | 435 | 458 | 0.69 | 6.24 | 6.16 | 0.72 | 0.42 |
1379| 0 | 456 | 516 | 0 | 0 | 0 | 432 | 459 | 0.67 | 6.12 | 6.09 | 0.71 | 0.44 |
1380| 0 | 457 | 463 | 0 | 0 | 0 | 397 | 415 | 0.72 | 7.19 | 7.19 | 0.73 | 0.41 |
1381| 0 | 458 | 539 | 0 | 0 | 0 | 459 | 478 | 0.71 | 7.03 | 7.07 | 0.73 | 0.43 |
1382| 0 | 459 | 471 | 0 | 0 | 0 | 400 | 424 | 0.67 | 6.38 | 6.31 | 0.71 | 0.44 |
1383| 0 | 460 | 468 | 0 | 0 | 0 | 400 | 420 | 0.68 | 6.55 | 6.94 | 0.71 | 0.46 |
1384| 0 | 461 | 509 | 0 | 0 | 0 | 436 | 454 | 0.63 | 6.01 | 5.8 | 0.71 | 0.43 |
1385| 0 | 462 | 545 | 0 | 0 | 0 | 454 | 475 | 0.71 | 6.17 | 6.29 | 0.72 | 0.41 |
1386| 0 | 463 | 544 | 0 | 0 | 0 | 468 | 486 | 0.67 | 6.87 | 6.84 | 0.71 | 0.45 |
1387| 0 | 464 | 526 | 0 | 0 | 0 | 444 | 464 | 0.65 | 6.15 | 6.08 | 0.71 | 0.42 |
1388| 0 | 465 | 515 | 0 | 0 | 0 | 447 | 463 | 0.7 | 6.68 | 6.7 | 0.72 | 0.44 |
1389| 0 | 466 | 513 | 0 | 0 | 0 | 444 | 459 | 0.67 | 7.41 | 7.27 | 0.71 | 0.42 |
1390| 0 | 467 | 521 | 0 | 0 | 0 | 436 | 457 | 0.64 | 6.14 | 6.43 | 0.71 | 0.44 |
1391| 0 | 468 | 455 | 0 | 0 | 0 | 381 | 399 | 0.72 | 7.15 | 6.95 | 0.72 | 0.43 |
1392| 0 | 469 | 560 | 0 | 0 | 0 | 481 | 500 | 0.72 | 6.43 | 6.42 | 0.73 | 0.42 |
1393| 0 | 470 | 489 | 0 | 0 | 0 | 419 | 431 | 0.76 | 7.47 | 7.58 | 0.73 | 0.42 |
1394| 0 | 471 | 448 | 0 | 0 | 0 | 386 | 402 | 0.68 | 5.78 | 5.87 | 0.72 | 0.41 |
1395| 0 | 472 | 507 | 0 | 0 | 0 | 421 | 436 | 0.64 | 6.17 | 6.13 | 0.7 | 0.42 |
1396| 0 | 473 | 579 | 0 | 0 | 0 | 499 | 516 | 0.67 | 6.75 | 6.58 | 0.72 | 0.42 |
1397| 0 | 474 | 497 | 0 | 0 | 0 | 431 | 447 | 0.64 | 5.41 | 5.36 | 0.72 | 0.42 |
1398| 0 | 475 | 535 | 0 | 0 | 0 | 458 | 473 | 0.65 | 6.39 | 6.23 | 0.71 | 0.42 |
1399| 0 | 476 | 499 | 0 | 0 | 0 | 408 | 429 | 0.68 | 6.67 | 6.56 | 0.72 | 0.46 |
1400| 0 | 477 | 504 | 0 | 0 | 0 | 422 | 437 | 0.71 | 6.61 | 6.52 | 0.72 | 0.43 |
1401| 0 | 478 | 501 | 0 | 0 | 0 | 429 | 450 | 0.71 | 7.09 | 7.09 | 0.73 | 0.42 |
1402| 0 | 479 | 522 | 0 | 0 | 0 | 453 | 472 | 0.76 | 7.15 | 7.22 | 0.72 | 0.43 |
1403| 0 | 480 | 464 | 0 | 0 | 0 | 402 | 418 | 0.71 | 6.36 | 6.26 | 0.72 | 0.44 |
1404| 0 | 481 | 497 | 0 | 0 | 0 | 425 | 449 | 0.64 | 5.49 | 5.52 | 0.7 | 0.44 |
1405| 0 | 482 | 560 | 0 | 0 | 0 | 479 | 498 | 0.73 | 6.14 | 6.14 | 0.72 | 0.45 |
1406| 0 | 483 | 510 | 0 | 0 | 0 | 419 | 438 | 0.67 | 5.43 | 5.42 | 0.71 | 0.44 |
1407| 0 | 484 | 515 | 0 | 0 | 0 | 445 | 464 | 0.68 | 6.56 | 6.41 | 0.71 | 0.45 |
1408| 0 | 485 | 514 | 0 | 0 | 0 | 432 | 454 | 0.75 | 6.78 | 6.66 | 0.72 | 0.42 |
1409| 0 | 486 | 505 | 0 | 0 | 0 | 435 | 451 | 0.69 | 6.27 | 6.22 | 0.73 | 0.41 |
1410| 0 | 487 | 506 | 0 | 0 | 0 | 435 | 460 | 0.65 | 5.52 | 5.72 | 0.73 | 0.44 |
1411| 0 | 488 | 469 | 0 | 0 | 0 | 398 | 413 | 0.73 | 6.64 | 6.6 | 0.71 | 0.46 |
1412| 0 | 489 | 507 | 0 | 0 | 0 | 427 | 441 | 0.65 | 6.06 | 5.87 | 0.7 | 0.45 |
1413| 0 | 490 | 512 | 0 | 0 | 0 | 436 | 450 | 0.69 | 5.51 | 5.4 | 0.73 | 0.44 |
1414| 0 | 491 | 546 | 0 | 0 | 0 | 461 | 479 | 0.72 | 6.78 | 6.64 | 0.71 | 0.44 |
1415| 0 | 492 | 505 | 0 | 0 | 0 | 432 | 453 | 0.66 | 6.06 | 5.94 | 0.7 | 0.44 |
1416| 0 | 493 | 503 | 0 | 0 | 0 | 429 | 446 | 0.75 | 7.42 | 7.42 | 0.73 | 0.43 |
1417| 0 | 494 | 508 | 0 | 0 | 0 | 441 | 452 | 0.71 | 6 | 5.95 | 0.73 | 0.43 |
1418| 0 | 495 | 521 | 0 | 0 | 0 | 444 | 459 | 0.72 | 7.32 | 7.16 | 0.72 | 0.41 |
1419| 0 | 496 | 474 | 0 | 0 | 0 | 403 | 421 | 0.68 | 5.48 | 5.41 | 0.71 | 0.45 |
1420| 0 | 497 | 541 | 0 | 0 | 0 | 473 | 489 | 0.71 | 6.02 | 5.88 | 0.72 | 0.44 |
1421| 0 | 498 | 523 | 0 | 0 | 0 | 438 | 456 | 0.72 | 6.65 | 6.57 | 0.72 | 0.44 |
1422| 0 | 499 | 497 | 0 | 0 | 0 | 428 | 444 | 0.67 | 5.44 | 5.33 | 0.71 | 0.45 |
1423| 0 | 500 | 518 | 0 | 0 | 0 | 434 | 450 | 0.71 | 6.11 | 5.9 | 0.7 | 0.46 |
1424| 0 | 501 | 522 | 0 | 0 | 0 | 449 | 467 | 0.75 | 6.94 | 6.83 | 0.73 | 0.41 |
1425| 0 | 502 | 490 | 0 | 0 | 0 | 427 | 439 | 0.72 | 5.94 | 5.92 | 0.72 | 0.45 |
1426| 0 | 503 | 499 | 0 | 0 | 0 | 421 | 439 | 0.72 | 6.89 | 6.79 | 0.72 | 0.45 |
1427| 0 | 504 | 480 | 0 | 0 | 0 | 407 | 425 | 0.71 | 5.9 | 5.92 | 0.72 | 0.44 |
1428| 0 | 505 | 549 | 0 | 0 | 0 | 487 | 506 | 0.73 | 6.42 | 6.33 | 0.72 | 0.44 |
1429| 0 | 506 | 500 | 0 | 0 | 0 | 423 | 443 | 0.71 | 6.93 | 6.86 | 0.71 | 0.45 |
1430| 0 | 507 | 502 | 0 | 0 | 0 | 429 | 447 | 0.75 | 7.67 | 7.52 | 0.73 | 0.41 |
1431| 0 | 508 | 544 | 0 | 0 | 0 | 464 | 485 | 0.8 | 7.05 | 7.12 | 0.73 | 0.42 |
1432| 0 | 509 | 485 | 0 | 0 | 0 | 416 | 429 | 0.74 | 6.53 | 6.48 | 0.72 | 0.45 |
1433| 0 | 510 | 516 | 0 | 0 | 0 | 441 | 458 | 0.77 | 6.24 | 6.16 | 0.73 | 0.43 |
1434| 0 | 511 | 486 | 0 | 0 | 0 | 419 | 438 | 0.72 | 6.07 | 5.98 | 0.72 | 0.45 |
1435| 0 | 512 | 522 | 0 | 0 | 0 | 454 | 474 | 0.71 | 5.49 | 5.54 | 0.71 | 0.42 |
1436| 0 | 513 | 507 | 0 | 0 | 0 | 433 | 446 | 0.77 | 6.4 | 6.27 | 0.72 | 0.44 |
1437| 0 | 514 | 535 | 0 | 0 | 0 | 458 | 474 | 0.78 | 6.32 | 6.47 | 0.72 | 0.44 |
1438| 0 | 515 | 492 | 0 | 0 | 0 | 433 | 451 | 0.78 | 6.36 | 6.41 | 0.73 | 0.43 |
1439| 0 | 516 | 493 | 0 | 0 | 0 | 417 | 440 | 0.78 | 6.91 | 6.72 | 0.72 | 0.43 |
1440| 0 | 517 | 525 | 0 | 0 | 0 | 434 | 450 | 0.79 | 6.44 | 6.39 | 0.73 | 0.41 |
1441| 0 | 518 | 504 | 0 | 0 | 0 | 434 | 456 | 0.8 | 7.15 | 7.06 | 0.72 | 0.43 |
1442| 0 | 519 | 533 | 0 | 0 | 0 | 464 | 482 | 0.79 | 7.03 | 6.93 | 0.72 | 0.43 |
1443| 0 | 520 | 508 | 0 | 0 | 0 | 413 | 433 | 0.77 | 6.81 | 6.62 | 0.73 | 0.41 |
1444| 0 | 521 | 520 | 0 | 0 | 0 | 436 | 454 | 0.81 | 6.47 | 6.38 | 0.73 | 0.43 |
1445| 0 | 522 | 484 | 1 | 0 | 0 | 403 | 424 | 0.75 | 6.09 | 6.13 | 0.72 | 0.43 |
1446| 0 | 523 | 503 | 0 | 0 | 0 | 438 | 455 | 0.77 | 5.89 | 5.78 | 0.73 | 0.42 |
1447| 0 | 524 | 521 | 0 | 0 | 0 | 444 | 462 | 0.81 | 6.22 | 6.14 | 0.73 | 0.44 |
1448| 0 | 525 | 519 | 0 | 0 | 0 | 449 | 469 | 0.8 | 5.88 | 5.79 | 0.73 | 0.44 |
1449| 0 | 526 | 515 | 0 | 0 | 0 | 447 | 465 | 0.77 | 6.55 | 6.44 | 0.73 | 0.44 |
1450| 0 | 527 | 492 | 0 | 0 | 0 | 418 | 443 | 0.76 | 5.93 | 5.85 | 0.73 | 0.43 |
1451| 0 | 528 | 502 | 0 | 0 | 0 | 420 | 442 | 0.85 | 6.55 | 6.44 | 0.74 | 0.4 |
1452| 0 | 529 | 512 | 2 | 0 | 0 | 452 | 468 | 0.82 | 7 | 6.89 | 0.72 | 0.42 |
1453| 0 | 530 | 513 | 0 | 0 | 0 | 435 | 454 | 0.74 | 6.1 | 6.1 | 0.72 | 0.44 |
1454| 0 | 531 | 512 | 2 | 0 | 0 | 441 | 466 | 0.84 | 6.36 | 6.26 | 0.73 | 0.41 |
1455| 0 | 532 | 519 | 0 | 0 | 0 | 452 | 464 | 0.86 | 7.33 | 7.24 | 0.74 | 0.41 |
1456| 0 | 533 | 515 | 0 | 0 | 0 | 438 | 451 | 0.83 | 6.13 | 6.16 | 0.72 | 0.45 |
1457| 0 | 534 | 482 | 0 | 0 | 0 | 409 | 429 | 0.84 | 7.19 | 7 | 0.73 | 0.41 |
1458| 0 | 535 | 516 | 0 | 0 | 0 | 427 | 449 | 0.81 | 6.68 | 6.43 | 0.73 | 0.42 |
1459| 0 | 536 | 502 | 0 | 0 | 0 | 434 | 453 | 0.86 | 6.76 | 6.64 | 0.73 | 0.41 |
1460| 0 | 537 | 512 | 0 | 0 | 0 | 435 | 453 | 0.79 | 6.21 | 6.06 | 0.73 | 0.42 |
1461| 0 | 538 | 511 | 2 | 0 | 0 | 430 | 451 | 0.79 | 6.34 | 6.21 | 0.74 | 0.41 |
1462| 0 | 539 | 506 | 0 | 0 | 0 | 430 | 450 | 0.87 | 6.83 | 6.97 | 0.73 | 0.41 |
1463| 0 | 540 | 503 | 0 | 0 | 0 | 429 | 444 | 0.87 | 6.34 | 6.24 | 0.73 | 0.43 |
1464| 0 | 541 | 518 | 8 | 0 | 0 | 446 | 460 | 0.87 | 6.51 | 6.45 | 0.74 | 0.41 |
1465| 0 | 542 | 503 | 29 | 0 | 0 | 450 | 467 | 0.89 | 7.38 | 7.53 | 0.73 | 0.41 |
1466| 0 | 543 | 491 | 16 | 0 | 0 | 425 | 441 | 0.83 | 5.91 | 6.11 | 0.73 | 0.43 |
1467| 0 | 544 | 509 | 11 | 0 | 0 | 435 | 460 | 0.86 | 6.76 | 6.56 | 0.74 | 0.42 |
1468| 0 | 545 | 519 | 2 | 0 | 0 | 443 | 461 | 0.92 | 6.54 | 6.45 | 0.74 | 0.4 |
1469| 0 | 546 | 492 | 0 | 0 | 0 | 417 | 435 | 0.85 | 6.02 | 5.86 | 0.74 | 0.42 |
1470| 0 | 547 | 528 | 0 | 0 | 0 | 440 | 462 | 0.87 | 6.73 | 6.69 | 0.74 | 0.41 |
1471| 0 | 548 | 471 | 2 | 0 | 0 | 408 | 426 | 0.86 | 6.25 | 6.18 | 0.73 | 0.42 |
1472| 0 | 549 | 510 | 0 | 0 | 0 | 440 | 458 | 0.9 | 6.92 | 6.8 | 0.74 | 0.42 |
1473| 0 | 550 | 531 | 0 | 0 | 0 | 438 | 459 | 0.93 | 8.48 | 8.22 | 0.74 | 0.39 |
1474| 0 | 551 | 502 | 0 | 0 | 0 | 434 | 451 | 0.95 | 6.73 | 6.55 | 0.74 | 0.42 |
1475| 0 | 552 | 538 | 0 | 0 | 0 | 460 | 482 | 0.88 | 6.35 | 6.24 | 0.74 | 0.43 |
1476| 0 | 553 | 503 | 0 | 0 | 0 | 419 | 438 | 0.87 | 5.99 | 5.99 | 0.75 | 0.4 |
1477| 0 | 554 | 493 | 0 | 0 | 0 | 423 | 441 | 0.92 | 6.79 | 6.72 | 0.75 | 0.4 |
1478| 0 | 555 | 521 | 0 | 0 | 0 | 446 | 461 | 1.03 | 8.15 | 8.18 | 0.75 | 0.41 |
1479| 0 | 556 | 503 | 0 | 0 | 0 | 429 | 447 | 0.97 | 7.35 | 7.26 | 0.75 | 0.41 |
1480| 0 | 557 | 498 | 4 | 0 | 0 | 425 | 442 | 0.98 | 7.42 | 7.22 | 0.75 | 0.39 |
1481| 0 | 558 | 510 | 0 | 0 | 0 | 426 | 450 | 0.87 | 6.59 | 6.47 | 0.75 | 0.4 |
1482| 0 | 559 | 508 | 0 | 0 | 0 | 422 | 442 | 0.94 | 6.74 | 6.61 | 0.75 | 0.42 |
1483| 0 | 560 | 504 | 0 | 0 | 0 | 441 | 458 | 0.94 | 7.12 | 6.84 | 0.75 | 0.39 |
1484| 0 | 561 | 507 | 0 | 0 | 0 | 442 | 459 | 0.95 | 6.67 | 6.63 | 0.75 | 0.4 |
1485| 0 | 562 | 532 | 0 | 0 | 0 | 453 | 473 | 1 | 6.78 | 6.68 | 0.76 | 0.4 |
1486| 0 | 563 | 505 | 0 | 0 | 0 | 423 | 442 | 1.03 | 8.14 | 7.89 | 0.75 | 0.4 |
1487| 0 | 564 | 499 | 0 | 0 | 0 | 425 | 448 | 0.98 | 6.47 | 6.32 | 0.75 | 0.42 |
1488| 0 | 565 | 509 | 0 | 0 | 0 | 432 | 457 | 0.97 | 7.01 | 7.16 | 0.75 | 0.4 |
1489| 0 | 566 | 537 | 0 | 0 | 0 | 462 | 480 | 0.96 | 6.48 | 6.28 | 0.76 | 0.39 |
1490| 0 | 567 | 463 | 0 | 0 | 0 | 397 | 419 | 1.06 | 7.62 | 7.45 | 0.76 | 0.41 |
1491| 0 | 568 | 509 | 0 | 0 | 0 | 424 | 449 | 1.02 | 6.84 | 6.79 | 0.75 | 0.4 |
1492| 0 | 569 | 509 | 0 | 0 | 0 | 427 | 449 | 1.02 | 7.7 | 7.36 | 0.76 | 0.4 |
1493| 0 | 570 | 529 | 0 | 0 | 0 | 447 | 465 | 1.1 | 8.15 | 8.05 | 0.76 | 0.41 |
1494| 0 | 571 | 497 | 0 | 0 | 0 | 423 | 445 | 1.06 | 6.71 | 6.89 | 0.76 | 0.43 |
1495| 0 | 572 | 532 | 0 | 0 | 0 | 444 | 468 | 1 | 5.99 | 6 | 0.76 | 0.41 |
1496| 0 | 573 | 498 | 0 | 0 | 0 | 431 | 452 | 1.14 | 7.77 | 7.83 | 0.77 | 0.39 |
1497| 0 | 574 | 500 | 0 | 0 | 0 | 408 | 432 | 1.01 | 6.12 | 5.9 | 0.76 | 0.42 |
1498| 0 | 575 | 505 | 0 | 0 | 0 | 430 | 445 | 1.15 | 8.01 | 7.82 | 0.77 | 0.4 |
1499| 0 | 576 | 502 | 0 | 0 | 0 | 441 | 455 | 1.04 | 6.33 | 6.38 | 0.76 | 0.4 |
1500| 0 | 577 | 516 | 0 | 0 | 0 | 432 | 459 | 1.1 | 7.19 | 7.02 | 0.77 | 0.38 |
1501| 0 | 578 | 498 | 0 | 0 | 0 | 412 | 428 | 1.12 | 7.35 | 7.33 | 0.76 | 0.41 |
1502| 0 | 579 | 530 | 0 | 0 | 0 | 462 | 482 | 1.15 | 6.38 | 6.73 | 0.77 | 0.41 |
1503| 0 | 580 | 484 | 0 | 0 | 0 | 421 | 429 | 1.04 | 5.94 | 5.92 | 0.76 | 0.42 |
1504| 0 | 581 | 532 | 0 | 0 | 0 | 460 | 478 | 1.21 | 8.1 | 7.98 | 0.78 | 0.4 |
1505| 0 | 582 | 503 | 0 | 0 | 0 | 422 | 448 | 1.19 | 8.48 | 8.2 | 0.77 | 0.42 |
1506| 0 | 583 | 500 | 0 | 0 | 0 | 425 | 444 | 1.16 | 7.46 | 7.32 | 0.78 | 0.39 |
1507| 0 | 584 | 524 | 0 | 0 | 0 | 440 | 457 | 1.23 | 7.66 | 7.57 | 0.77 | 0.4 |
1508| 0 | 585 | 505 | 0 | 0 | 0 | 436 | 450 | 1.26 | 7.17 | 7.03 | 0.79 | 0.4 |
1509| 0 | 586 | 517 | 0 | 0 | 0 | 433 | 456 | 1.13 | 6.1 | 6.23 | 0.77 | 0.41 |
1510| 0 | 587 | 496 | 0 | 0 | 0 | 428 | 442 | 1.33 | 8.48 | 8.38 | 0.79 | 0.38 |
1511| 0 | 588 | 513 | 0 | 0 | 0 | 438 | 453 | 1.22 | 7.8 | 7.87 | 0.78 | 0.38 |
1512| 0 | 589 | 510 | 0 | 0 | 0 | 438 | 460 | 1.34 | 8.37 | 8.4 | 0.79 | 0.39 |
1513| 0 | 590 | 508 | 0 | 0 | 0 | 441 | 464 | 1.25 | 7.64 | 7.41 | 0.78 | 0.38 |
1514| 0 | 591 | 505 | 0 | 0 | 0 | 435 | 449 | 1.25 | 6.6 | 6.48 | 0.79 | 0.4 |
1515| 0 | 592 | 497 | 0 | 0 | 0 | 427 | 441 | 1.3 | 8.13 | 8.1 | 0.78 | 0.39 |
1516| 0 | 593 | 525 | 0 | 0 | 0 | 438 | 459 | 1.39 | 8.25 | 8.15 | 0.79 | 0.38 |
1517| 0 | 594 | 506 | 0 | 0 | 0 | 435 | 455 | 1.23 | 6.76 | 6.63 | 0.78 | 0.4 |
1518| 0 | 595 | 525 | 0 | 0 | 0 | 442 | 460 | 1.32 | 7.1 | 7.06 | 0.79 | 0.39 |
1519| 0 | 596 | 487 | 0 | 0 | 0 | 418 | 438 | 1.26 | 6.86 | 6.63 | 0.78 | 0.39 |
1520| 0 | 597 | 504 | 0 | 0 | 0 | 430 | 449 | 1.48 | 9.76 | 9.67 | 0.8 | 0.39 |
1521| 0 | 598 | 504 | 0 | 0 | 0 | 431 | 447 | 1.42 | 7.86 | 7.72 | 0.79 | 0.39 |
1522| 0 | 599 | 522 | 0 | 0 | 0 | 439 | 456 | 1.31 | 6.19 | 6.14 | 0.79 | 0.38 |
1523| 0 | 600 | 514 | 0 | 0 | 0 | 457 | 471 | 1.29 | 8.24 | 8.06 | 0.79 | 0.37 |
1524| 0 | 601 | 527 | 0 | 0 | 0 | 456 | 474 | 1.45 | 9.29 | 9.02 | 0.8 | 0.39 |
1525| 0 | 602 | 485 | 0 | 0 | 0 | 413 | 427 | 1.32 | 8.23 | 8.06 | 0.79 | 0.39 |
1526| 0 | 603 | 513 | 0 | 0 | 0 | 442 | 460 | 1.54 | 9.02 | 8.95 | 0.8 | 0.38 |
1527| 0 | 604 | 520 | 0 | 0 | 0 | 429 | 451 | 1.35 | 7.46 | 7.51 | 0.79 | 0.39 |
1528| 0 | 605 | 513 | 0 | 0 | 0 | 432 | 450 | 1.46 | 6.87 | 6.73 | 0.8 | 0.38 |
1529| 0 | 606 | 510 | 0 | 0 | 0 | 428 | 454 | 1.35 | 7.37 | 7.21 | 0.79 | 0.39 |
1530| 0 | 607 | 509 | 0 | 0 | 0 | 432 | 455 | 1.39 | 8.23 | 8.18 | 0.79 | 0.39 |
1531| 0 | 608 | 491 | 0 | 0 | 0 | 412 | 435 | 1.42 | 8.22 | 8 | 0.8 | 0.36 |
1532| 0 | 609 | 526 | 0 | 0 | 0 | 452 | 468 | 1.48 | 8.07 | 7.89 | 0.8 | 0.39 |
1533| 0 | 610 | 489 | 0 | 0 | 0 | 427 | 444 | 1.41 | 9.18 | 9 | 0.79 | 0.39 |
1534| 0 | 611 | 531 | 0 | 0 | 0 | 456 | 465 | 1.39 | 7.89 | 7.88 | 0.79 | 0.4 |
1535| 0 | 612 | 488 | 0 | 0 | 0 | 419 | 436 | 1.3 | 6.03 | 6.24 | 0.79 | 0.39 |
1536| 0 | 613 | 496 | 0 | 0 | 0 | 423 | 432 | 1.37 | 7.32 | 7.31 | 0.8 | 0.36 |
1537| 0 | 614 | 519 | 0 | 0 | 0 | 448 | 472 | 1.45 | 8.24 | 8.07 | 0.79 | 0.39 |
1538| 0 | 615 | 493 | 0 | 0 | 0 | 431 | 446 | 1.37 | 7.1 | 6.94 | 0.79 | 0.37 |
1539| 0 | 616 | 529 | 0 | 0 | 0 | 445 | 472 | 1.35 | 7.78 | 7.71 | 0.79 | 0.37 |
1540| 0 | 617 | 525 | 0 | 0 | 0 | 443 | 465 | 1.4 | 8.2 | 8.17 | 0.79 | 0.4 |
1541| 0 | 618 | 499 | 0 | 0 | 0 | 414 | 444 | 1.36 | 7.67 | 7.55 | 0.79 | 0.38 |
1542| 0 | 619 | 528 | 0 | 0 | 0 | 455 | 477 | 1.39 | 8.1 | 7.86 | 0.79 | 0.39 |
1543| 0 | 620 | 503 | 0 | 0 | 0 | 429 | 439 | 1.34 | 7.93 | 7.97 | 0.79 | 0.39 |
1544| 0 | 621 | 485 | 0 | 0 | 0 | 415 | 435 | 1.33 | 7.18 | 7.1 | 0.79 | 0.41 |
1545| 0 | 622 | 502 | 0 | 0 | 0 | 426 | 438 | 1.28 | 7.04 | 6.95 | 0.79 | 0.41 |
1546| 0 | 623 | 517 | 0 | 0 | 0 | 441 | 457 | 1.29 | 7.54 | 7.35 | 0.78 | 0.39 |
1547| 0 | 624 | 500 | 0 | 0 | 0 | 417 | 443 | 1.31 | 8.65 | 8.49 | 0.79 | 0.38 |
1548| 0 | 625 | 503 | 0 | 0 | 0 | 430 | 453 | 1.21 | 8.33 | 7.95 | 0.78 | 0.4 |
1549| 0 | 626 | 529 | 0 | 0 | 0 | 447 | 465 | 1.25 | 6.84 | 6.64 | 0.78 | 0.41 |
1550| 0 | 627 | 521 | 0 | 0 | 0 | 434 | 466 | 1.38 | 9.23 | 8.89 | 0.79 | 0.37 |
1551| 0 | 628 | 509 | 0 | 0 | 0 | 433 | 451 | 1.3 | 8.23 | 7.99 | 0.79 | 0.39 |
1552| 0 | 629 | 504 | 0 | 0 | 0 | 433 | 446 | 1.23 | 8.81 | 8.77 | 0.77 | 0.41 |
1553| 0 | 630 | 513 | 0 | 0 | 0 | 438 | 453 | 1.29 | 7.51 | 7.37 | 0.78 | 0.4 |
1554| 0 | 631 | 516 | 0 | 0 | 0 | 432 | 450 | 1.1 | 6.33 | 6.14 | 0.78 | 0.38 |
1555| 0 | 632 | 519 | 0 | 0 | 0 | 446 | 468 | 1.19 | 9.43 | 9.26 | 0.77 | 0.41 |
1556| 0 | 633 | 483 | 0 | 0 | 0 | 419 | 432 | 1.16 | 7.96 | 7.84 | 0.77 | 0.4 |
1557| 0 | 634 | 510 | 0 | 0 | 0 | 440 | 460 | 1.21 | 7.61 | 7.55 | 0.77 | 0.4 |
1558| 0 | 635 | 483 | 0 | 0 | 0 | 403 | 420 | 1.23 | 9.51 | 9.24 | 0.77 | 0.4 |
1559| 0 | 636 | 529 | 0 | 0 | 0 | 443 | 461 | 1.13 | 7.23 | 7.12 | 0.77 | 0.41 |
1560| 0 | 637 | 514 | 0 | 0 | 0 | 451 | 467 | 1.08 | 7.75 | 7.51 | 0.76 | 0.41 |
1561| 0 | 638 | 492 | 0 | 0 | 0 | 414 | 430 | 1.11 | 8.31 | 8.04 | 0.76 | 0.43 |
1562| 0 | 639 | 539 | 0 | 0 | 0 | 449 | 470 | 1.11 | 6.87 | 6.73 | 0.76 | 0.42 |
1563| 0 | 640 | 506 | 0 | 0 | 0 | 444 | 456 | 1.24 | 9.43 | 9.19 | 0.77 | 0.39 |
1564| 0 | 641 | 477 | 0 | 0 | 0 | 410 | 431 | 1.01 | 7.75 | 7.38 | 0.76 | 0.42 |
1565| 0 | 642 | 530 | 0 | 0 | 0 | 452 | 471 | 1.03 | 7.66 | 7.58 | 0.75 | 0.44 |
1566| 0 | 643 | 500 | 0 | 0 | 0 | 412 | 434 | 1.04 | 6.99 | 6.75 | 0.76 | 0.4 |
1567| 0 | 644 | 520 | 0 | 0 | 0 | 451 | 468 | 1.1 | 6.94 | 6.95 | 0.76 | 0.41 |
1568| 0 | 645 | 515 | 0 | 0 | 0 | 428 | 453 | 1.14 | 7.29 | 7.23 | 0.77 | 0.39 |
1569| 0 | 646 | 486 | 0 | 0 | 0 | 413 | 429 | 1 | 6.9 | 6.68 | 0.76 | 0.42 |
1570| 0 | 647 | 536 | 0 | 0 | 0 | 449 | 465 | 1.03 | 7.76 | 7.64 | 0.75 | 0.43 |
1571| 0 | 648 | 485 | 0 | 0 | 0 | 407 | 426 | 0.97 | 6.87 | 6.59 | 0.75 | 0.42 |
1572| 0 | 649 | 506 | 0 | 0 | 0 | 443 | 455 | 1.02 | 8.04 | 7.91 | 0.75 | 0.41 |
1573| 0 | 650 | 494 | 0 | 0 | 0 | 422 | 439 | 1.04 | 7.23 | 7.08 | 0.75 | 0.39 |
1574| 0 | 651 | 520 | 0 | 0 | 0 | 456 | 473 | 1.04 | 8.13 | 8.53 | 0.76 | 0.41 |
1575| 0 | 652 | 511 | 0 | 0 | 0 | 433 | 455 | 0.96 | 8.52 | 8.18 | 0.74 | 0.42 |
1576| 0 | 653 | 507 | 0 | 0 | 0 | 428 | 440 | 1.01 | 7.82 | 7.61 | 0.75 | 0.4 |
1577| 0 | 654 | 524 | 0 | 0 | 0 | 442 | 462 | 0.96 | 7.42 | 7.36 | 0.75 | 0.41 |
1578| 0 | 655 | 490 | 0 | 0 | 0 | 427 | 441 | 0.94 | 6.61 | 6.63 | 0.74 | 0.43 |
1579| 0 | 656 | 497 | 0 | 0 | 0 | 422 | 436 | 0.96 | 7.18 | 7.13 | 0.74 | 0.41 |
1580| 0 | 657 | 518 | 0 | 0 | 0 | 432 | 455 | 0.91 | 6.84 | 6.67 | 0.74 | 0.4 |
1581| 0 | 658 | 516 | 0 | 0 | 0 | 440 | 456 | 0.98 | 7.82 | 7.8 | 0.74 | 0.4 |
1582| 0 | 659 | 521 | 0 | 0 | 0 | 443 | 468 | 0.96 | 9 | 8.54 | 0.74 | 0.42 |
1583| 0 | 660 | 482 | 0 | 0 | 0 | 408 | 421 | 0.93 | 8.25 | 8.22 | 0.74 | 0.39 |
1584| 0 | 661 | 535 | 0 | 0 | 0 | 475 | 491 | 0.96 | 8.22 | 8.08 | 0.74 | 0.43 |
1585| 0 | 662 | 509 | 0 | 0 | 0 | 433 | 450 | 0.81 | 5.39 | 5.35 | 0.73 | 0.4 |
1586| 0 | 663 | 513 | 0 | 0 | 0 | 444 | 459 | 0.96 | 8.4 | 8.25 | 0.73 | 0.43 |
1587| 0 | 664 | 487 | 0 | 0 | 0 | 418 | 428 | 0.93 | 7.24 | 7.35 | 0.74 | 0.43 |
1588| 0 | 665 | 529 | 0 | 0 | 0 | 453 | 469 | 0.94 | 7.22 | 7.02 | 0.73 | 0.41 |
1589| 0 | 666 | 509 | 0 | 0 | 0 | 436 | 455 | 0.85 | 6.34 | 6.28 | 0.73 | 0.42 |
1590| 0 | 667 | 510 | 0 | 0 | 0 | 446 | 462 | 0.86 | 6.69 | 6.47 | 0.74 | 0.41 |
1591| 0 | 668 | 494 | 0 | 0 | 0 | 419 | 436 | 0.96 | 8.39 | 8.27 | 0.74 | 0.44 |
1592| 0 | 669 | 520 | 0 | 0 | 0 | 443 | 457 | 0.81 | 6.23 | 6.16 | 0.73 | 0.41 |
1593| 0 | 670 | 513 | 0 | 0 | 0 | 432 | 448 | 0.85 | 6.66 | 6.69 | 0.73 | 0.43 |
1594| 0 | 671 | 483 | 0 | 0 | 0 | 409 | 426 | 0.91 | 8.37 | 8.27 | 0.73 | 0.41 |
1595| 0 | 672 | 502 | 1 | 0 | 0 | 447 | 463 | 0.87 | 7.17 | 6.98 | 0.74 | 0.4 |
1596| 0 | 673 | 538 | 0 | 0 | 0 | 465 | 481 | 0.9 | 7.7 | 7.53 | 0.73 | 0.42 |
1597| 0 | 674 | 502 | 0 | 0 | 0 | 425 | 440 | 0.85 | 7.84 | 7.73 | 0.74 | 0.41 |
1598| 0 | 675 | 532 | 0 | 0 | 0 | 454 | 471 | 0.83 | 7.22 | 7.04 | 0.72 | 0.41 |
1599| 0 | 676 | 496 | 1 | 0 | 0 | 419 | 430 | 0.78 | 7.18 | 7.06 | 0.72 | 0.43 |
1600| 0 | 677 | 504 | 0 | 0 | 0 | 427 | 447 | 0.87 | 7.81 | 7.76 | 0.73 | 0.42 |
1601| 0 | 678 | 475 | 0 | 0 | 0 | 399 | 416 | 0.89 | 8.11 | 8.02 | 0.73 | 0.41 |
1602| 0 | 679 | 541 | 0 | 0 | 0 | 457 | 475 | 0.86 | 7.3 | 7.16 | 0.74 | 0.41 |
1603| 0 | 680 | 503 | 0 | 0 | 0 | 426 | 450 | 0.84 | 7.25 | 6.98 | 0.73 | 0.41 |
1604| 0 | 681 | 526 | 0 | 0 | 0 | 445 | 470 | 0.84 | 7.01 | 6.75 | 0.73 | 0.43 |
1605| 0 | 682 | 474 | 0 | 0 | 0 | 383 | 407 | 0.82 | 7.37 | 7.3 | 0.72 | 0.42 |
1606| 0 | 683 | 571 | 0 | 0 | 0 | 476 | 501 | 0.75 | 6.83 | 6.85 | 0.71 | 0.45 |
1607| 0 | 684 | 451 | 0 | 0 | 0 | 390 | 404 | 0.94 | 9.59 | 9.37 | 0.75 | 0.39 |
1608| 0 | 685 | 524 | 0 | 0 | 0 | 451 | 463 | 0.85 | 7.42 | 7.29 | 0.74 | 0.43 |
1609| 0 | 686 | 507 | 0 | 0 | 0 | 435 | 460 | 0.83 | 7.51 | 7.33 | 0.73 | 0.41 |
1610| 0 | 687 | 502 | 0 | 0 | 0 | 416 | 437 | 0.79 | 7.81 | 7.51 | 0.72 | 0.42 |
1611| 0 | 688 | 501 | 0 | 0 | 0 | 423 | 443 | 0.79 | 7.34 | 7.15 | 0.72 | 0.44 |
1612| 0 | 689 | 560 | 0 | 0 | 0 | 470 | 487 | 0.74 | 6.75 | 6.64 | 0.7 | 0.46 |
1613| 0 | 690 | 523 | 0 | 0 | 0 | 454 | 477 | 0.82 | 7.68 | 7.59 | 0.73 | 0.42 |
1614| 0 | 691 | 458 | 0 | 0 | 0 | 405 | 420 | 0.8 | 6.96 | 6.79 | 0.72 | 0.42 |
1615| 0 | 692 | 505 | 0 | 0 | 0 | 415 | 444 | 0.78 | 7.18 | 6.98 | 0.72 | 0.43 |
1616| 0 | 693 | 500 | 0 | 0 | 0 | 436 | 450 | 0.78 | 7.27 | 7.3 | 0.73 | 0.41 |
1617| 0 | 694 | 526 | 0 | 0 | 0 | 455 | 471 | 0.79 | 7.17 | 6.98 | 0.72 | 0.42 |
1618| 0 | 695 | 507 | 0 | 0 | 0 | 411 | 432 | 0.73 | 7.04 | 6.75 | 0.72 | 0.43 |
1619| 0 | 696 | 532 | 0 | 0 | 0 | 462 | 476 | 0.71 | 6.75 | 6.76 | 0.71 | 0.46 |
1620| 0 | 697 | 506 | 0 | 0 | 0 | 413 | 426 | 0.86 | 8.03 | 7.98 | 0.73 | 0.42 |
1621| 0 | 698 | 505 | 1 | 0 | 0 | 437 | 456 | 0.78 | 7.17 | 7.09 | 0.71 | 0.44 |
1622| 0 | 699 | 495 | 0 | 0 | 0 | 421 | 434 | 0.81 | 6.96 | 7.14 | 0.73 | 0.45 |
1623| 0 | 700 | 487 | 0 | 0 | 0 | 408 | 429 | 0.79 | 7.44 | 7.26 | 0.72 | 0.43 |
1624| 0 | 701 | 538 | 0 | 0 | 0 | 461 | 480 | 0.79 | 7.22 | 7.09 | 0.73 | 0.45 |
1625| 0 | 702 | 509 | 0 | 0 | 0 | 452 | 467 | 0.7 | 6.16 | 6.08 | 0.71 | 0.44 |
1626| 0 | 703 | 526 | 0 | 0 | 0 | 454 | 474 | 0.72 | 6.58 | 6.37 | 0.72 | 0.42 |
1627| 0 | 704 | 487 | 0 | 0 | 0 | 413 | 433 | 0.73 | 6.17 | 6.06 | 0.72 | 0.42 |
1628| 0 | 705 | 500 | 1 | 0 | 0 | 437 | 452 | 0.79 | 7.45 | 7.39 | 0.72 | 0.42 |
1629| 0 | 706 | 496 | 0 | 0 | 0 | 396 | 420 | 0.73 | 6.92 | 6.67 | 0.72 | 0.44 |
1630| 0 | 707 | 531 | 0 | 0 | 0 | 450 | 466 | 0.72 | 6.88 | 6.96 | 0.71 | 0.45 |
1631| 0 | 708 | 515 | 1 | 0 | 0 | 448 | 461 | 0.78 | 7.08 | 6.91 | 0.73 | 0.4 |
1632| 0 | 709 | 516 | 0 | 0 | 0 | 442 | 458 | 0.72 | 7.38 | 7.29 | 0.71 | 0.46 |
1633| 0 | 710 | 525 | 0 | 0 | 0 | 435 | 464 | 0.71 | 6.62 | 6.49 | 0.71 | 0.46 |
1634| 0 | 711 | 504 | 0 | 0 | 0 | 426 | 445 | 0.82 | 7.95 | 8.03 | 0.73 | 0.43 |
1635| 0 | 712 | 499 | 1 | 0 | 0 | 417 | 442 | 0.77 | 7.6 | 7.39 | 0.72 | 0.44 |
1636| 0 | 713 | 467 | 3 | 0 | 0 | 402 | 420 | 0.73 | 7.66 | 7.44 | 0.73 | 0.41 |
1637| 0 | 714 | 515 | 0 | 0 | 0 | 446 | 456 | 0.75 | 8.06 | 7.92 | 0.73 | 0.44 |
1638| 0 | 715 | 518 | 1 | 0 | 0 | 442 | 466 | 0.7 | 6.26 | 6.17 | 0.72 | 0.45 |
1639| 0 | 716 | 519 | 0 | 0 | 0 | 445 | 463 | 0.74 | 7.34 | 7.28 | 0.72 | 0.43 |
1640| 0 | 717 | 538 | 4 | 0 | 0 | 461 | 479 | 0.67 | 6.7 | 6.65 | 0.72 | 0.43 |
1641| 0 | 718 | 525 | 5 | 0 | 0 | 448 | 470 | 0.73 | 7.13 | 6.96 | 0.71 | 0.43 |
1642| 0 | 719 | 448 | 12 | 0 | 0 | 400 | 415 | 0.72 | 6.17 | 6.11 | 0.71 | 0.47 |
1643| 0 | 720 | 271 | 209 | 0 | 0 | 406 | 421 | 0.76 | 7.98 | 8.47 | 0.73 | 0.5 |
1644+------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------+
1645
1646 Summary vs resolution
1647+------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------+
1648| ID | d min | # full | # part | # over | # ice | # sum | # prf | Ibg | I/sigI | I/sigI | CC prf | RMSD XY |
1649| | | | | | | | | | (sum) | (prf) | | |
1650|------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------|
1651| 0 | 1.21 | 377 | 3 | 0 | 0 | 192 | 316 | 0.08 | 0.26 | 0.19 | 0.5 | 0.98 |
1652| 0 | 1.23 | 1335 | 10 | 0 | 0 | 956 | 1230 | 0.09 | 0.26 | 0.22 | 0.51 | 0.92 |
1653| 0 | 1.25 | 3233 | 22 | 0 | 0 | 2604 | 2964 | 0.1 | 0.27 | 0.24 | 0.52 | 0.87 |
1654| 0 | 1.28 | 5312 | 39 | 0 | 0 | 4367 | 4820 | 0.12 | 0.32 | 0.28 | 0.53 | 0.8 |
1655| 0 | 1.3 | 7648 | 52 | 0 | 0 | 6426 | 6910 | 0.13 | 0.41 | 0.36 | 0.55 | 0.74 |
1656| 0 | 1.33 | 11090 | 74 | 0 | 0 | 9246 | 9877 | 0.15 | 0.46 | 0.41 | 0.56 | 0.69 |
1657| 0 | 1.36 | 15376 | 93 | 0 | 0 | 12968 | 13817 | 0.18 | 0.54 | 0.47 | 0.58 | 0.63 |
1658| 0 | 1.4 | 20780 | 131 | 0 | 0 | 17867 | 18839 | 0.21 | 0.64 | 0.56 | 0.6 | 0.59 |
1659| 0 | 1.43 | 23748 | 169 | 0 | 0 | 20757 | 21527 | 0.25 | 0.74 | 0.66 | 0.62 | 0.55 |
1660| 0 | 1.48 | 24455 | 177 | 0 | 0 | 20309 | 21234 | 0.28 | 1 | 0.9 | 0.64 | 0.51 |
1661| 0 | 1.52 | 24341 | 172 | 0 | 0 | 20600 | 21461 | 0.32 | 1.28 | 1.18 | 0.66 | 0.47 |
1662| 0 | 1.58 | 24576 | 171 | 0 | 0 | 21431 | 22116 | 0.37 | 1.57 | 1.47 | 0.69 | 0.44 |
1663| 0 | 1.64 | 24704 | 186 | 0 | 0 | 21130 | 21778 | 0.43 | 1.93 | 1.84 | 0.72 | 0.41 |
1664| 0 | 1.72 | 25053 | 171 | 0 | 0 | 21340 | 21965 | 0.52 | 2.71 | 2.61 | 0.76 | 0.38 |
1665| 0 | 1.81 | 25183 | 188 | 0 | 0 | 21644 | 22283 | 0.66 | 3.85 | 3.79 | 0.8 | 0.35 |
1666| 0 | 1.92 | 25090 | 237 | 0 | 0 | 21766 | 22213 | 0.89 | 5.77 | 5.76 | 0.84 | 0.32 |
1667| 0 | 2.07 | 25616 | 181 | 0 | 0 | 22279 | 22783 | 1.15 | 8.1 | 8.17 | 0.87 | 0.31 |
1668| 0 | 2.28 | 25697 | 178 | 0 | 0 | 22616 | 23009 | 1.39 | 11.22 | 11.42 | 0.89 | 0.26 |
1669| 0 | 2.61 | 26130 | 179 | 0 | 0 | 22426 | 22950 | 2.12 | 18.05 | 18.41 | 0.89 | 0.25 |
1670| 0 | 3.28 | 26279 | 244 | 0 | 0 | 22936 | 23274 | 3.59 | 41.78 | 42.63 | 0.87 | 0.24 |
1671+------+---------+----------+----------+----------+---------+---------+---------+-------+----------+----------+----------+-----------+
1672
1673 Summary for experiment 0
1674+---------------------------------------+-----------+----------+--------+
1675| Item | Overall | Low | High |
1676|---------------------------------------+-----------+----------+--------|
1677| dmin | 1.21 | 3.28 | 1.21 |
1678| dmax | 69.3 | 69.3 | 1.23 |
1679| number fully recorded | 366023 | 26279 | 377 |
1680| number partially recorded | 2677 | 244 | 3 |
1681| number with invalid background pixels | 95794 | 5244 | 369 |
1682| number with invalid foreground pixels | 54404 | 3550 | 188 |
1683| number with overloaded pixels | 0 | 0 | 0 |
1684| number in powder rings | 0 | 0 | 0 |
1685| number processed with summation | 313860 | 22936 | 192 |
1686| number processed with profile fitting | 325366 | 23274 | 316 |
1687| number failed in background modelling | 1557 | 647 | 0 |
1688| number failed in summation | 54404 | 3550 | 188 |
1689| number failed in profile fitting | 42898 | 3212 | 64 |
1690| ibg | 0.87 | 3.59 | 0.08 |
1691| i/sigi (summation) | 7.1 | 41.78 | 0.26 |
1692| i/sigi (profile fitting) | 7.04 | 42.63 | 0.19 |
1693| cc prf | 0.74 | 0.87 | 0.5 |
1694| cc_pearson sum/prf | 1 | 1 | 0.65 |
1695| cc_spearman sum/prf | 0.95 | 1 | 0.54 |
1696+---------------------------------------+-----------+----------+--------+
1697
1698Timing information for integration
1699+-------------------+----------------+
1700| Read time | 51.99 seconds |
1701| Extract time | 2.81 seconds |
1702| Pre-process time | 0.47 seconds |
1703| Process time | 146.55 seconds |
1704| Post-process time | 0.00 seconds |
1705| Total time | 202.56 seconds |
1706+-------------------+----------------+
1707
1708Removing 41645 unintegrated reflections of 368700 total
1709Saving 327055 reflections to integrated.refl
1710Saving the experiments to integrated.expt
Checking the log output, we see that after loading in the reference
reflections from refined.refl, new predictions are made up to the
highest resolution at the corner of the detector. This is fine, but if we
wanted to we could have adjusted the resolution limits using parameters
prediction.d_min and prediction.d_max. The predictions are
made using the scan-varying crystal model recorded in
refined.expt. This ensures that prediction is made using
the smoothly varying lattice and orientation that we determined in the
refinement step. As this scan-varying model was determined in advance of
integration, each of the integration jobs is independent and we can take
advantage of true parallelism during processing.
The profile model is calculated from the reflections in
refined.refl. First reflections with a too small ‘zeta’
factor are filtered out. This essentially removes reflections that are too
close to the spindle axis. In general these reflections require significant
Lorentz corrections and as a result have less trustworthy intensities anyway.
From the remaining reflection shoeboxes, the average beam divergence and
reflecting range is calculated, providing the two Gaussian width parameters
\(\sigma_D\) and \(\sigma_M\) used in the 3D profile model.
Following this, independent integration jobs are set up. These jobs overlap, so reflections are assigned to one or more jobs. What follows are blocks of information specific to each integration job.
After these jobs are finished, the reflections are ‘post-processed’, which includes the application of the LP correction to the intensities. Then summary tables are printed giving quality statistics first by frame, and then by resolution bin.
Symmetry analysis¶
After integration, further assessments of the crystal symmetry are possible. Previously, we made an assessment of the lattice symmetry (i.e. the symmetry of the diffraction spot positions), however now we have determined a set of intensity values and can investigate the full symmetry of the diffraction pattern (i.e. spot positions and intensities). The symmetry analysis consists of two stages, determining the laue group symmetry and analysing absent reflections to suggest the space group symmetry.
dials.symmetry integrated.expt integrated.refl
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3
4input {
5 experiments = integrated.expt
6 reflections = integrated.refl
7}
8
9================================================================================
10
11Performing Laue group analysis
12
13Mapping all input cells to a common minimum cell
14Filtering reflections for dataset 0
15Read 327055 predicted reflections
16Selected 312171 reflections integrated by profile and summation methods
17Combined 37 partial reflections with other partial reflections
18Removed 12 reflections below partiality threshold
19Removed 0 intensity.sum.value reflections with I/Sig(I) < -5
20Removed 0 intensity.prf.value reflections with I/Sig(I) < -5
21A round of outlier rejection has been performed,
22147 outliers have been identified.
23
24Patterson group: C 1 2/m 1 (x-y,x+y,z)
25
26--------------------------------------------------------------------------------
27
28Normalising intensities for dataset 1
29
30ML estimate of overall B_cart value:
31 14.53, -0.86, -1.19
32 14.01, -0.88
33 10.83
34ML estimate of -log of scale factor:
35 -2.16
36
37--------------------------------------------------------------------------------
38
39Estimation of resolution for Laue group analysis
40
41Removing 2 Wilson outliers with E^2 >= 16.0
42Resolution estimate from <I>/<σ(I)> > 4.0 : 2.07
43Resolution estimate from CC½ > 0.60: 1.40
44High resolution limit set to: 1.40
45Selecting 156273 reflections with d > 1.40
46
47Input crystal symmetry:
48Unit cell: (40.5512, 40.5512, 69.2879, 91.9959, 91.9959, 98.0722)
49Space group: P 1 (No. 1)
50Change of basis op to minimum cell: -b,-a,-c
51Crystal symmetry in minimum cell:
52Unit cell: (40.5512, 40.5512, 69.2879, 91.9959, 91.9959, 98.0722)
53Space group: P 1 (No. 1)
54Lattice point group: C 1 2/m 1 (x-y,x+y,z)
55
56Overall CC for 20000 unrelated pairs: 0.388
57Estimated expectation value of true correlation coefficient E(CC) = 0.927
58Estimated sd(CC) = 0.686 / sqrt(N)
59Estimated E(CC) of true correlation coefficient from identity = 0.961
60
61--------------------------------------------------------------------------------
62
63Scoring individual symmetry elements
64
65+--------------+--------+------+--------+-----+---------------+
66| likelihood | Z-CC | CC | N | | Operator |
67|--------------+--------+------+--------+-----+---------------|
68| 0.929 | 9.93 | 0.99 | 152014 | *** | 1 |(0, 0, 0) |
69| 0.927 | 9.83 | 0.98 | 151282 | *** | 2 |(-1, 1, 0) |
70+--------------+--------+------+--------+-----+---------------+
71
72--------------------------------------------------------------------------------
73
74Scoring all possible sub-groups
75
76+-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------+
77| Patterson group | | Likelihood | NetZcc | Zcc+ | Zcc- | CC | CC- | delta | Reindex operator |
78|-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------|
79| C 1 2/m 1 | *** | 0.927 | 9.88 | 9.88 | 0 | 0.99 | 0 | 0 | -a-b,-a+b,-c |
80| P -1 | | 0.073 | 0.1 | 9.93 | 9.83 | 0.99 | 0.98 | 0 | a,b,c |
81+-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------+
82
83Best solution: C 1 2/m 1
84Unit cell: 53.169, 61.242, 69.288, 90.000, 93.045, 90.000
85Reindex operator: -a-b,-a+b,-c
86Laue group probability: 0.927
87Laue group confidence: 0.890
88
89+-------------------+--------------------------+
90| Patterson group | Corresponding MX group |
91|-------------------+--------------------------|
92| C 1 2/m 1 | C 1 2 1 |
93+-------------------+--------------------------+
94================================================================================
95
96Analysing systematic absences
97
98Laue group: C 1 2/m 1
99No absences to check for this laue group
100
101Saving reindexed experiments to symmetrized.expt in space group C 1 2 1
102Saving 327055 reindexed reflections to symmetrized.refl
The laue group symmetry is the 3D rotational symmetry of the diffraction pattern plus inversion symmetry (due to Friedel’s law that I(h,k,l) = I(-h,-k,-l) when absorption is negligible). To determine the laue group symmetry, all possible symmetry operations of the lattice are scored by comparing the correlation of reflection intensities that would be equivalent under a given operation. The scores for individual symmetry operations are then combined to score the potential laue groups.
Scoring all possible sub-groups
+-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------+
| Patterson group | | Likelihood | NetZcc | Zcc+ | Zcc- | CC | CC- | delta | Reindex operator |
|-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------|
| C 1 2/m 1 | *** | 0.927 | 9.88 | 9.88 | 0 | 0.99 | 0 | 0 | -a-b,-a+b,-c |
| P -1 | | 0.073 | 0.1 | 9.93 | 9.83 | 0.99 | 0.98 | 0 | a,b,c |
+-------------------+-----+--------------+----------+--------+--------+------+-------+---------+--------------------+
Best solution: C 1 2/m 1
Unit cell: 53.169, 61.242, 69.288, 90.000, 93.045, 90.000
Reindex operator: -a-b,-a+b,-c
Laue group probability: 0.927
Laue group confidence: 0.890
+-------------------+--------------------------+
| Patterson group | Corresponding MX group |
|-------------------+--------------------------|
| C 1 2/m 1 | C 1 2 1 |
+-------------------+--------------------------+
================================================================================
Here we see clearly that the best solution is given by C 1 2/m 1, with
a high likelihood. For macromolecules, their chirality means that mirror symmetry
is not allowed (the ‘m’ in C 1 2/m 1), therefore the determined symmetry
relevant for MX at this point is C2. For some laue groups, there are multiple
space groups possible due additional translational symmetries
(e.g P 2, P 21 for laue group P2/m), which requires an additional
analysis of systematic absences. However this is not the case for C 1 2/m 1,
therefore the final result of the analysis is the space group C2, in agreement
with the result from dials.refine_bravais_settings.
Scaling and Merging¶
Before the data can be reduced for structure solution, the intensity values must be corrected for experimental effects which occur prior to the reflection being measured on the detector. These primarily include sample illumination/absorption effects and radiation damage, which result in symmetry-equivalent reflections having unequal measured intensities (i.e. a systematic effect in addition to any variance due to counting statistics). Thus the purpose of scaling is to determine a scale factor to apply to each reflection, such that the scaled intensities are representative of the ‘true’ scattering intensity from the contents of the unit cell.
During scaling, a scaling model is created, from which scale factors are calculated for each reflection. Three physically motivated corrections are used to create an scaling model, in a similar manner to that used in the program aimless. This model consists of a smoothly varying scale factor as a function of rotation angle, a smoothly varying B-factor to account for radiation damage as a function of rotation angle and an absorption surface correction, dependent on the direction of the incoming and scattered beam vector relative to the crystal.
dials.scale symmetrized.expt symmetrized.refl
Show/Hide Log
1DIALS 3.dev.1293-g7efd2982c
2The following parameters have been modified:
3input {
4 experiments = symmetrized.expt
5 reflections = symmetrized.refl
6}
7
8Checking for the existence of a reflection table
9containing multiple datasets
10
11Found 1 reflection tables & 1 experiments in total.
12
13Dataset ids are: 0
14
15Space group being used during scaling is C 1 2 1
16
17Scaling models have been initialised for all experiments.
18
19================================================================================
20
21The experiment id for this dataset is 0.
22The scaling model type being applied is physical.
23
24Applying filter of min_isigi > -5.0, partiality > 0.4
25Read 327055 predicted reflections
26Selected 327055 reflections integrated by profile or summation methods
27Removed 1097 reflections below partiality threshold
28Removed 0 intensity.sum.value reflections with I/Sig(I) < -5.0
29Removed 0 intensity.prf.value reflections with I/Sig(I) < -5.0
30Combined 37 partial reflections with other partial reflections
31Excluding 1658/327018 reflections
32Reflections passing individual criteria:
33criterion: user excluded, reflections: 1658
34criterion: excluded for scaling, reflections: 1658
35
36The following corrections will be applied to this dataset:
37
38+--------------+----------------+
39| correction | n_parameters |
40|--------------+----------------|
41| scale | 26 |
42| decay | 20 |
43| absorption | 24 |
44+--------------+----------------+
45Loaded error model:
46Error model details:
47 Type: basic
48 Parameters: a = 1.00000, b = 0.02000
49 Error model formula: σ'² = a²(σ² + (bI)²)
50 estimated I/sigma asymptotic limit: 50.000
51
52A round of outlier rejection has been performed,
536495 outliers have been identified.
54
55325057 reflections were preselected for scale factor determination
56out of 325360 suitable reflections:
57Reflections passing individual criteria:
58criterion: in I/sigma range (I/sig > -5.0), reflections: 325360
59criterion: above min partiality ( > 0.95), reflections: 325057
60
61Randomly selected 7479/48533 groups (m>1) to use for scaling model
62minimisation (50267 reflections)
63Completed preprocessing and initialisation for this dataset.
64
65================================================================================
66
67Components to be refined in this cycle for all datasets: scale, decay, absorption
68Performing a round of scaling with an LBFGS minimizer.
69
70Time taken for refinement 3.51
71
72Refinement steps:
73+--------+--------+----------+
74| Step | Nref | RMSD_I |
75| | | (a.u) |
76|--------+--------+----------|
77| 0 | 49239 | 1.2229 |
78| 1 | 49239 | 1.1741 |
79| 2 | 49239 | 1.0486 |
80| 3 | 49239 | 0.98302 |
81| 4 | 49239 | 0.88602 |
82| 5 | 49239 | 0.83634 |
83| 6 | 49239 | 0.83311 |
84| 7 | 49239 | 0.81495 |
85| 8 | 49239 | 0.80991 |
86| 9 | 49239 | 0.80024 |
87| 10 | 49239 | 0.79652 |
88| 11 | 49239 | 0.79593 |
89| 12 | 49239 | 0.79519 |
90| 13 | 49239 | 0.79502 |
91| 14 | 49239 | 0.79476 |
92| 15 | 49239 | 0.79467 |
93| 16 | 49239 | 0.79456 |
94| 17 | 49239 | 0.79446 |
95| 18 | 49239 | 0.79439 |
96+--------+--------+----------+
97RMSD no longer decreasing
98lbfgs minimizer stop: callback_after_step is True
99
100================================================================================
101
102Scale factors determined during minimisation have now been
103applied to all reflections for dataset 0.
104
105A round of outlier rejection has been performed,
106174 outliers have been identified.
107
108Performing profile/summation intensity optimisation.
109+----------------+---------+---------+
110| Combination | CC1/2 | Rmeas |
111|----------------+---------+---------|
112| prf only | 0.99899 | 0.06032 |
113| sum only | 0.99889 | 0.06693 |
114| Imid = 310.18 | 0.99901 | 0.06024 |
115| Imid = 39732.8 | 0.99899 | 0.06032 |
116| Imid = 3973.28 | 0.999 | 0.06024 |
117| Imid = 397.33 | 0.99901 | 0.06015 |
118| Imid = 39.73 | 0.99892 | 0.06294 |
119+----------------+---------+---------+
120Combined intensities with Imid = 397.33 determined to be best for scaling.
121
122A round of outlier rejection has been performed,
123145 outliers have been identified.
124
125Components to be refined in this cycle for all datasets: scale, decay, absorption
126Performing a round of scaling with an LBFGS minimizer.
127
128Time taken for refinement 1.82
129
130Refinement steps:
131+--------+--------+----------+
132| Step | Nref | RMSD_I |
133| | | (a.u) |
134|--------+--------+----------|
135| 0 | 50237 | 0.8316 |
136| 1 | 50237 | 0.83105 |
137| 2 | 50237 | 0.82988 |
138| 3 | 50237 | 0.82979 |
139| 4 | 50237 | 0.82947 |
140| 5 | 50237 | 0.82931 |
141| 6 | 50237 | 0.8291 |
142| 7 | 50237 | 0.82898 |
143| 8 | 50237 | 0.82897 |
144+--------+--------+----------+
145RMSD no longer decreasing
146lbfgs minimizer stop: callback_after_step is True
147
148================================================================================
149
150Scale factors determined during minimisation have now been
151applied to all reflections for dataset 0.
152
153A round of outlier rejection has been performed,
154136 outliers have been identified.
155
156Performing a round of error model refinement.
157
158Error model details:
159 Type: basic
160 Parameters: a = 0.70558, b = 0.03851
161 Error model formula: σ'² = a²(σ² + (bI)²)
162 estimated I/sigma asymptotic limit: 36.803
163
164Results of error model refinement. Uncorrected and corrected variances
165of normalised intensity deviations for given intensity ranges. Variances
166are expected to be ~1.0 for reliable errors (sigmas).
167+--------------------------+----------+------------------------+----------------------+
168| Intensity range (<Ih>) | n_refl | Uncorrected variance | Corrected variance |
169|--------------------------+----------+------------------------+----------------------|
170| 9940.92 - 1929.89 | 883 | 9.372 | 0.899 |
171| 1929.89 - 1464.25 | 883 | 7.5 | 1.099 |
172| 1464.25 - 1234.05 | 883 | 5.049 | 1.045 |
173| 1234.05 - 907.13 | 2075 | 3.976 | 0.978 |
174| 907.13 - 498.58 | 5971 | 2.692 | 1.096 |
175| 498.58 - 274.03 | 9784 | 1.576 | 1.124 |
176| 274.03 - 150.61 | 14793 | 1.015 | 1.128 |
177| 150.61 - 82.78 | 19598 | 0.743 | 1.092 |
178| 82.78 - 45.50 | 20571 | 0.582 | 0.999 |
179| 45.50 - 25.00 | 12898 | 0.472 | 0.87 |
180+--------------------------+----------+------------------------+----------------------+
181
182Components to be refined in this cycle for all datasets: scale, decay, absorption
183Performing a round of scaling with a Levenberg-Marquardt minimizer.
184
185Time taken for refinement 3.55
186
187Refinement steps:
188+--------+--------+----------+
189| Step | Nref | RMSD_I |
190| | | (a.u) |
191|--------+--------+----------|
192| 0 | 50241 | 1.0462 |
193| 1 | 50241 | 1.0429 |
194| 2 | 50241 | 1.0403 |
195| 3 | 50241 | 1.0388 |
196| 4 | 50241 | 1.0385 |
197| 5 | 50241 | 1.0385 |
198+--------+--------+----------+
199RMSD no longer decreasing
200
201================================================================================
202
203Components to be refined in this cycle for all datasets: scale, decay, absorption
204Performing a round of scaling with a Levenberg-Marquardt minimizer.
205
206Time taken for refinement 1.12
207
208Refinement steps:
209+--------+--------+----------+
210| Step | Nref | RMSD_I |
211| | | (a.u) |
212|--------+--------+----------|
213| 0 | 50241 | 1.0385 |
214| 1 | 50241 | 1.0385 |
215+--------+--------+----------+
216RMSD no longer decreasing
217
218================================================================================
219
220Scale factors determined during minimisation have now been
221applied to all reflections for dataset 0.
222
223A round of outlier rejection has been performed,
224194 outliers have been identified.
225
226Performing a round of error model refinement.
227
228Error model details:
229 Type: basic
230 Parameters: a = 0.67987, b = 0.04165
231 Error model formula: σ'² = a²(σ² + (bI)²)
232 estimated I/sigma asymptotic limit: 35.315
233
234Results of error model refinement. Uncorrected and corrected variances
235of normalised intensity deviations for given intensity ranges. Variances
236are expected to be ~1.0 for reliable errors (sigmas).
237+--------------------------+----------+------------------------+----------------------+
238| Intensity range (<Ih>) | n_refl | Uncorrected variance | Corrected variance |
239|--------------------------+----------+------------------------+----------------------|
240| 9948.35 - 1933.82 | 881 | 10.818 | 0.982 |
241| 1933.82 - 1469.59 | 881 | 7.716 | 1.084 |
242| 1469.59 - 1237.97 | 881 | 4.995 | 0.986 |
243| 1237.97 - 907.54 | 2095 | 4.068 | 0.904 |
244| 907.54 - 498.76 | 5998 | 2.68 | 1.04 |
245| 498.76 - 274.11 | 9803 | 1.534 | 1.088 |
246| 274.11 - 150.64 | 14766 | 0.987 | 1.104 |
247| 150.64 - 82.79 | 19580 | 0.724 | 1.098 |
248| 82.79 - 45.50 | 20436 | 0.558 | 1.009 |
249| 45.50 - 25.00 | 12833 | 0.463 | 0.907 |
250+--------------------------+----------+------------------------+----------------------+
251
252
253The reflection table variances have been adjusted to account for the
254uncertainty in the scaling model
255
256Total time taken: 19.2424s
257
258================================================================================
259
26040.00% of model parameters have significant uncertainty
261(sigma/abs(parameter) > 0.5)
262
263Summary of dataset partialities
264+------------------+----------+
265| Partiality (p) | n_refl |
266|------------------+----------|
267| all reflections | 327018 |
268| p > 0.99 | 324965 |
269| 0.5 < p < 0.99 | 352 |
270| 0.01 < p < 0.5 | 333 |
271| p < 0.01 | 1368 |
272+------------------+----------+
273
274Reflections below a partiality_cutoff of 0.4 are not considered for any
275part of the scaling analysis or for the reporting of merging statistics.
276Additionally, if applicable, only reflections with a min_partiality > 0.95
277were considered for use when refining the scaling model.
278
279
280 ----------Merging statistics by resolution bin----------
281
282 d_max d_min #obs #uniq mult. %comp <I> <I/sI> r_mrg r_meas r_pim r_anom cc1/2 cc_ano
283 69.30 3.29 23039 3403 6.77 98.64 544.2 67.7 0.037 0.041 0.015 0.043 0.999* 0.281*
284 3.29 2.61 22762 3324 6.85 97.51 198.5 47.5 0.049 0.054 0.020 0.059 0.998* 0.311*
285 2.61 2.28 22907 3267 7.01 96.77 103.0 35.7 0.065 0.070 0.026 0.073 0.997* 0.364*
286 2.28 2.07 22692 3257 6.97 96.05 70.5 27.4 0.078 0.084 0.032 0.081 0.996* 0.260*
287 2.07 1.92 21994 3178 6.92 95.21 45.8 20.5 0.098 0.106 0.040 0.099 0.994* 0.226*
288 1.92 1.81 22184 3190 6.95 94.30 26.2 14.1 0.136 0.147 0.055 0.130 0.991* 0.174*
289 1.81 1.72 21827 3167 6.89 94.14 16.2 9.8 0.180 0.194 0.073 0.172 0.985* 0.139*
290 1.72 1.64 21503 3114 6.91 93.01 11.0 7.0 0.233 0.252 0.096 0.214 0.980* 0.095*
291 1.64 1.58 22175 3126 7.09 92.65 8.6 5.8 0.283 0.305 0.114 0.245 0.972* 0.100*
292 1.58 1.53 21424 3096 6.92 91.98 6.5 4.5 0.340 0.368 0.139 0.305 0.958* 0.084*
293 1.53 1.48 20941 3075 6.81 91.74 5.0 3.5 0.419 0.454 0.173 0.367 0.949* 0.007
294 1.48 1.44 21447 3035 7.07 90.73 3.6 2.6 0.559 0.603 0.225 0.461 0.921* 0.079*
295 1.44 1.40 19017 3009 6.32 90.44 3.1 2.1 0.635 0.692 0.271 0.566 0.889* 0.031
296 1.40 1.36 14339 2461 5.83 72.90 2.5 1.6 0.736 0.808 0.326 0.651 0.832* -0.014
297 1.36 1.33 9982 1762 5.67 52.58 2.2 1.4 0.843 0.925 0.374 0.745 0.790* -0.053
298 1.33 1.31 6957 1290 5.39 38.61 1.9 1.2 0.919 1.013 0.416 0.822 0.785* 0.081*
299 1.31 1.28 5115 999 5.12 29.76 1.5 0.9 1.223 1.357 0.572 1.028 0.600* 0.015
300 1.28 1.26 3118 715 4.36 21.31 1.4 0.7 1.397 1.577 0.708 1.145 0.515* -0.020
301 1.26 1.23 1338 416 3.22 12.52 1.1 0.5 1.455 1.719 0.890 1.364 0.372* 0.016
302 1.23 1.21 405 233 1.74 6.87 1.0 0.4 0.984 1.271 0.793 1.264 0.630* 0.129
303 69.19 1.21 325166 49117 6.62 72.96 71.1 16.8 0.066 0.071 0.027 0.071 0.999* 0.314*
304
305
306
307 -------------Summary of merging statistics--------------
308
309 Overall Low High
310High resolution limit 1.21 3.29 1.21
311Low resolution limit 69.19 69.30 1.23
312Completeness 73.0 98.6 6.9
313Multiplicity 6.6 6.8 1.7
314I/sigma 16.8 67.7 0.4
315Rmerge(I) 0.066 0.037 0.984
316Rmerge(I+/-) 0.056 0.031 0.964
317Rmeas(I) 0.071 0.041 1.271
318Rmeas(I+/-) 0.067 0.036 1.364
319Rpim(I) 0.027 0.015 0.793
320Rpim(I+/-) 0.035 0.019 0.964
321CC half 0.999 0.999 0.630
322Anomalous completeness 71.7 99.0 1.9
323Anomalous multiplicity 3.4 3.5 1.4
324Anomalous correlation 0.314 0.281 0.129
325Anomalous slope 1.089
326dF/F 0.063
327dI/s(dI) 1.226
328Total observations 325166 23039 405
329Total unique 49117 3403 233
330
331Writing html report to dials.scale.html
332Saving the scaled experiments to scaled.expt
333Saving the scaled reflections to scaled.refl
334See dials.github.io/dials_scale_user_guide.html for more info on scaling options
As can be seen from the output text, 70 parameters are used to parameterise the scaling model for this dataset. Outlier rejection is performed at several stages, as outliers have a disproportionately large effect during scaling and can lead to poor scaling results. During scaling, the distribution of the intensity uncertainties are also analysed and a correction is applied based on a prior expectation of the intensity error distribution. At the end of the output, a table and summary of the merging statistics are presented, which give indications of the quality of the scaled dataset:
----------Merging statistics by resolution bin----------
d_max d_min #obs #uniq mult. %comp <I> <I/sI> r_mrg r_meas r_pim r_anom cc1/2 cc_ano
69.30 3.29 23039 3403 6.77 98.64 544.2 67.7 0.037 0.041 0.015 0.043 0.999* 0.281*
3.29 2.61 22762 3324 6.85 97.51 198.5 47.5 0.049 0.054 0.020 0.059 0.998* 0.311*
2.61 2.28 22907 3267 7.01 96.77 103.0 35.7 0.065 0.070 0.026 0.073 0.997* 0.364*
2.28 2.07 22692 3257 6.97 96.05 70.5 27.4 0.078 0.084 0.032 0.081 0.996* 0.260*
2.07 1.92 21994 3178 6.92 95.21 45.8 20.5 0.098 0.106 0.040 0.099 0.994* 0.226*
1.92 1.81 22184 3190 6.95 94.30 26.2 14.1 0.136 0.147 0.055 0.130 0.991* 0.174*
1.81 1.72 21827 3167 6.89 94.14 16.2 9.8 0.180 0.194 0.073 0.172 0.985* 0.139*
1.72 1.64 21503 3114 6.91 93.01 11.0 7.0 0.233 0.252 0.096 0.214 0.980* 0.095*
1.64 1.58 22175 3126 7.09 92.65 8.6 5.8 0.283 0.305 0.114 0.245 0.972* 0.100*
1.58 1.53 21424 3096 6.92 91.98 6.5 4.5 0.340 0.368 0.139 0.305 0.958* 0.084*
1.53 1.48 20941 3075 6.81 91.74 5.0 3.5 0.419 0.454 0.173 0.367 0.949* 0.007
1.48 1.44 21447 3035 7.07 90.73 3.6 2.6 0.559 0.603 0.225 0.461 0.921* 0.079*
1.44 1.40 19017 3009 6.32 90.44 3.1 2.1 0.635 0.692 0.271 0.566 0.889* 0.031
1.40 1.36 14339 2461 5.83 72.90 2.5 1.6 0.736 0.808 0.326 0.651 0.832* -0.014
1.36 1.33 9982 1762 5.67 52.58 2.2 1.4 0.843 0.925 0.374 0.745 0.790* -0.053
1.33 1.31 6957 1290 5.39 38.61 1.9 1.2 0.919 1.013 0.416 0.822 0.785* 0.081*
1.31 1.28 5115 999 5.12 29.76 1.5 0.9 1.223 1.357 0.572 1.028 0.600* 0.015
1.28 1.26 3118 715 4.36 21.31 1.4 0.7 1.397 1.577 0.708 1.145 0.515* -0.020
1.26 1.23 1338 416 3.22 12.52 1.1 0.5 1.455 1.719 0.890 1.364 0.372* 0.016
1.23 1.21 405 233 1.74 6.87 1.0 0.4 0.984 1.271 0.793 1.264 0.630* 0.129
69.19 1.21 325166 49117 6.62 72.96 71.1 16.8 0.066 0.071 0.027 0.071 0.999* 0.314*
-------------Summary of merging statistics--------------
Overall Low High
High resolution limit 1.21 3.29 1.21
Low resolution limit 69.19 69.30 1.23
Completeness 73.0 98.6 6.9
Multiplicity 6.6 6.8 1.7
I/sigma 16.8 67.7 0.4
Rmerge(I) 0.066 0.037 0.984
Rmerge(I+/-) 0.056 0.031 0.964
Rmeas(I) 0.071 0.041 1.271
Rmeas(I+/-) 0.067 0.036 1.364
Rpim(I) 0.027 0.015 0.793
Rpim(I+/-) 0.035 0.019 0.964
CC half 0.999 0.999 0.630
Anomalous completeness 71.7 99.0 1.9
Anomalous multiplicity 3.4 3.5 1.4
Anomalous correlation 0.314 0.281 0.129
Anomalous slope 1.089
dF/F 0.063
dI/s(dI) 1.226
Total observations 325166 23039 405
Total unique 49117 3403 233
Looking at the resolution-dependent merging statistics, we can see that the completeness falls significantly beyond 1.4 Angstrom resolution. If desired, a resolution cutoff can be applied and the data rescaled (using the output of the previous scaling run as input to the next run to load the existing state of the scaling model):
dials.scale scaled.expt scaled.refl d_min=1.4
The merging statistics, as well as a number of scaling and merging plots, are
output into a html report called dials.scale.html.
This can be opened in your browser - nativigate to the section “scaling model plots” and take a look.
What is immediately apparent is the periodic nature of the scale term, with peaks
and troughs 90° apart. This indicates that the illuminated volume was changing
significantly during the experiment: a reflection would be measured as almost
twice as intense if it was measured at rotation angle of ~120° compared to at ~210°.
The absorption surface also shows a similar periodicity, as may be expected.
The relative B-factor shows low overall variation, suggesting little overall
radiation damage.
Once we are happy with the dataset quality, the final step of dials processing is to merge the data and produce a merged mtz file, suitable for input to downstream structure solution. To do this we can use the command:
dials.merge scaled.expt scaled.refl
The log output reports intensity statistics, the symmetry equivalent reflections are merged and a truncation procedure is performed, to give strictly positive merged structure factors (Fs) in addition to merged intensities.
HTML report¶
Much more information from the various steps of data processing can be found within an HTML report generated using the program dials.report. This is run simply with:
dials.report scaled.expt scaled.refl
which produces the file dials.report.html.
This report includes plots showing the scan-varying crystal orientation and unit cell parameters. The latter of these is useful to check that changes to the cell during processing appear reasonable. We can at least see from this and the low final refined RMSDs that this is a very well- behaved dataset.
Some of the most useful plots are
Difference between observed and calculated centroids vs phi, which shows how the average residuals in each of X, Y, and φ vary as a function of φ. If scan-varying refinement has been successful in capturing the real changes during the scan then we would expect these plots to be straight lines.
Centroid residuals in X and Y, in which the X, Y residuals are shown directly. The key point here is to look for a globular shape centred at the origin.
Difference between observed and calculated centroids in X and Y, which show the difference between predicted and observed reflection positions in either X or Y as functions of detector position. From these plots it is very easy to see whole tiles that are worse than their neighbours, and whether those tiles might be simply shifted or slightly rotated compared to the model detector.
Reflection and reference correlations binned in X/Y. These are useful companions to the plots of centroid residual as a function of detector position above. Whereas the above plots show systematic errors in the positions and orientations of tiles of a multi-panel detector, these plots indicate what effect that (and any other position-specific systematic error) has on the integrated data quality. The first of these plots shows the correlation between reflections and their reference profiles for all reflections in the dataset. The second shows only the correlations between the strong reference reflections and their profiles (thus these are expected to be higher and do not extend to such high resolution).
Distribution of I/Sigma vs Z. This reproduces the \(\frac{I}{\sigma_I}\) information versus frame number given in the log file in a graphical form. Here we see that \(\frac{I}{\sigma_I}\) is fairly flat over the whole dataset, which we might use as an indication that there were no bad frames, not much radiation damage occurred and that scale factors are likely to be fairly uniform.
Exporting to unmerged MTZ¶
It is possible that an unmerged mtz file is desired for further processing before
merging. To produce a scaled unmerged mtz file, one can use the dials.export
command on the scaled datafiles:
dials.export scaled.refl scaled.expt
It is also possible to export the integrated (unscaled) data in mtz
format using dials.export. If you have an installation of CCP4, symmetry
analysis and scaling can then be continued with the ccp4 programs
pointless, aimless and ctruncate to generate a merged mtz file:
dials.export integrated.refl integrated.expt
pointless hklin integrated.mtz hklout sorted.mtz > pointless.log
aimless hklin sorted.mtz hklout scaled.mtz > aimless.log << EOF
resolution 1.4
anomalous off
EOF
ctruncate -hklin scaled.mtz -hklout truncated.mtz \
-colin '/*/*/[IMEAN,SIGIMEAN]' > ctruncate.log
